Let f(x)=(xˣ-1) and g(x)=ln(x)+x-1. xˣ=e^(xln(x)). As x→0⁺, xˣ→1, while ln(x)→-∞, so f(x)/g(x)→0.
[f'(x)=ln(x)xˣ/x and g'(x)=(1/x)+1=(1+x)/x.
L'Hôpital's rule says we can use f'(x)/g'(x)=ln(x)xˣ/(1+x) with the same limit x→0⁺ in f(x)/g(x).
Note, however, that the expression cannot be evaluated for x<0, so the left limit cannot be evaluated. This may invalidate the use of l’Hôpital's rule.
The denominator approaches 1 in this limit. ln(x)→-∞ while xˣ→1. So under this rule the limit would be -∞.]
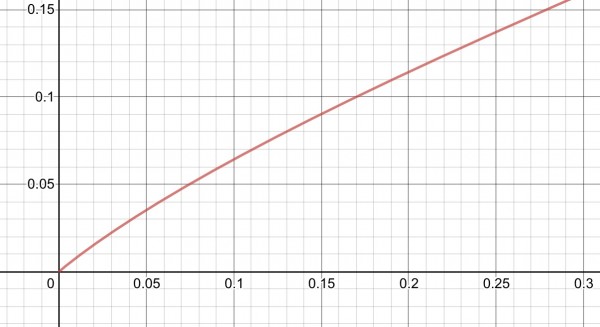
The graph above appears to show that the right limit is zero. Another way to find the limit is to set x to a small positive value and evaluate the expression. As x gets smaller, while remaining positive, the expression approaches zero.