The area of a rectangle is the product of two numbers, representing the length and width of the rectangle.
If the maximum perimeter is 20 and L and W represent the length and width, then the perimeter=2L+2W≤20.
Therefore L+W≤10. Also LW=A a constant area.
L+k/L≤10, L2+A≤10L, L2-10L≤-A, L2-10L+25≤25-A, (L-5)2-(25-A)≤0,
(L-5-√(25-A))(L-5+√(25-A))≤0.
Let A=16 (for example), then (L-5-3)(L-5+3)≤0, (L-8)(L-2)≤0, so L=8 or 2 is a solution (an 8 by 2 rectangle has an area of 16 square units and a perimeter of 20 units), but also:
L-8<0, L<8 and L-2>0, L>2, so 2<L<8. So, for example, L could be 3, 4, 5, 6 or 7, and W=16/3, 4, 16/5, 8/3 or 16/7.
If we pick four pairs of these values of L and W we have the dimensions of 4 rectangles. Also, L and W are interchangeable. Let's pick:
(L,W)=(16/3,3), (5,16/5), (6,8/3), (7,16/7). Note that (4,4) would be a square, so I've picked non-square rectangles.
The 4 rectangles with area 16 square units have dimensions:
length=5⅓, width=3; length=5, width=3.2; length=6, width=2⅔; length=7, width=22/7.
There are many other values that could have been used because we can choose any numbers, not just whole numbers, and we could have chosen a different area.
These four rectangles are shown below to scale:
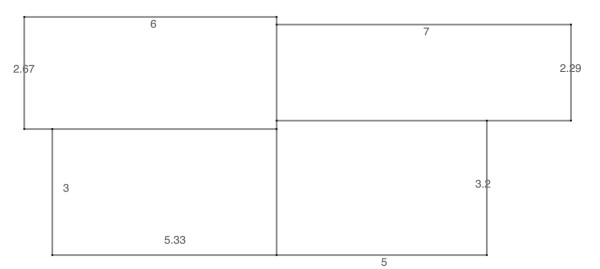
The dimensions of each rectangle are shown. All have the same area and different perimeters, not exceeding 20 units. Note that a rectangle with length=8 and width=2 also satisfies the requirements. Measurements are to two places of decimals.