what is the formula for sin(a+b)?

Question

sin (A+B)= sin A cos B + cos A sin B,how did they derived the answer?

Answer 1

 

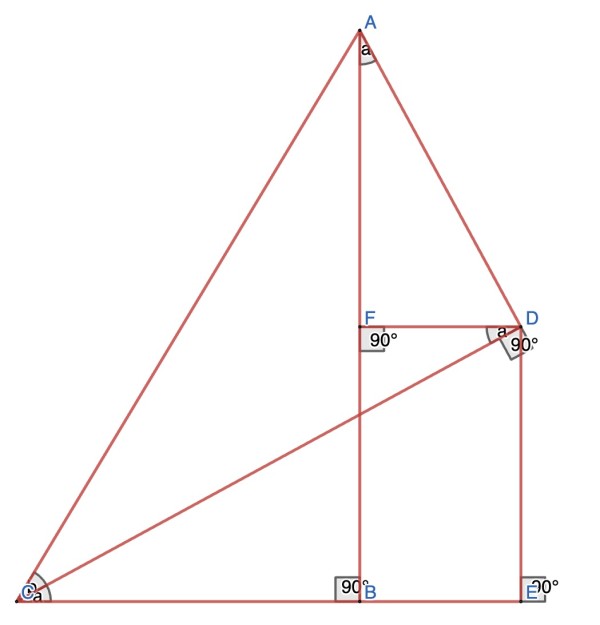
The picture shows right triangles ABC, ACD, DCE, AFD (some details may not be clear on the picture).

FDEB is a rectangle.

The following angles are relevant: AĈD=b, DĈB=DĈE=a, AĈB=AĈE=a+b. 

The geometry shows that FD̂C=FÂD=a. AB=AF+FB, but FB=DE so AB=AF+DE.

Therefore:

AB/AC=AF/AC+DE/AC. AF/AC=(AF/AD).(AD/AC) and DE/AC=(DE/DC).(DC/AC).

So AB/AC=sin(a+b)=(AF/AD).(AD/AC)+(DE/DC).(DC/AC)=cos(a)sin(b)+sin(a)cos(b).

Hence sin(a+b)=sin(a)cos(b)+cos(a)sin(b) QED.