Question

find all fourth roots of 81i

 

Answer 1

Let z⁴=81i, let z=re^iθ=r(cosθ+isinθ). [If z=a+ib, a=rcosθ, b=rsinθ.]

z⁴=r⁴e^4iθ=r⁴(cos(4θ)+isin(4θ))=81i.

r⁴=81, r=3; cos(4θ)+isin(4θ)=i, 4θ=(4n+1)π/2, θ=(4n+1)π/8 radians or (4n+1)22.5°.

z=3(cos((4n+1)π/8)+isin((4n+1)π/8).

n=0: z=3(cos(π/8)+isin(π/8));

n=1: z=3(cos(5π/8)+isin(3π/8));

n=2: z=3(cos(9π/8)+isin(5π/8));

n=3: z=3(cos(13π/8)+isin(7π/8));

Solution: z=2.7716386+1.1480503i, -1.1480503+2.7716386i, -2.7716386-1.1480503i, 1.1480503-2.7716386i approximately.

[cos(π/4)=2cos²(π/8)-1, cos²(π/8)=½(1+cos(π/4)), cos(π/8)=√(½(1+cos(π/4)))=√(½(1+√2/2)); sin²(π/8)=1-½(1+cos(π/4))=½(1-√2/2), sin(π/8)=√(½(1-√2/2)).]

ARGAND DIAGRAM

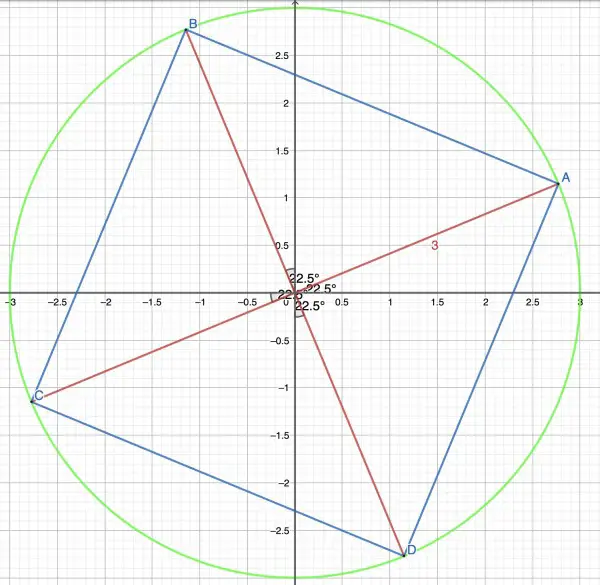
The four zeroes are shown as the points A, B, C, D. They form the sides of a square (blue), and the semi-diagonals (red) have a length (magnitude) of 3 showing that all the zeroes have magnitude 3 (4th root of 81), The green circle merely emphasises the constant magnitude. Note that the diagonals are inclined at an angle 22.5° (π/8).