We need two simultaneous equations. Assume that Chris and Joyce are travelling towards each other on the same road.
First, let 3pm be the our time base, so t=0 means 3pm and t=2 means 5pm.
If x is the distance they have travelled in time t, we have x=50t. By the time Joyce leaves home, Chris has travelled 100km.
Joyce is 2 hours behind Chris so x=540-60(t-2)=540-60t+120=660-60t.
t-2 signifies that time-zero for Joyce, that is, when t=2 (hours) Joyce is 540km away from Chris.
The two meet at some point (t,x) so we can write:
x=50t=660-60t.
5t=66-6t,
11t=66, t=6 hours, that is, 9pm.
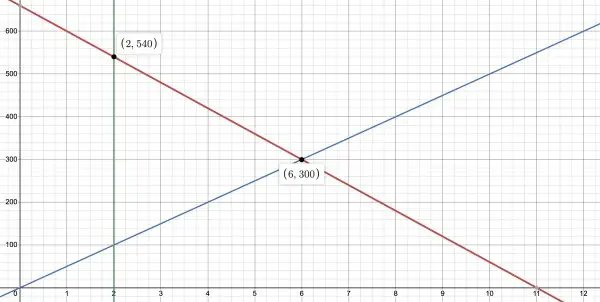
The graph represents the situation, with distance vertical and time horizontal. The gradients (slopes of the lines) represent their respective velocities. The red line is Joyce's path and the blue line Chris's path. The green line is t=2, showing that Joyce is 540km away from Chris at 5pm (2 hours after 3pm). As they travel towards each other you can see their relative positions until they meet at t=6 (9pm) 300km away from Chris's home. You can also see that at 5pm (t=2) Chris has travelled 100km.