y^3 dx+2(x^3-xy^2 )dy=0

Question

Ecuaciones diferenciales homogeneas

Answer 1

→ dy/dx=(y/x)^3 /2(y/x)^2 -2 → (1)

Answer 2

Transform:y/x

Answer 3

→ F(x)_=F:y'

Answer 4

→F+xF' → (2)

Answer 5

(1),(2)→ x dF/dx= F^3/2F^2-2 - F

Answer 6

→ x dF/dx=F(2-F^2)/2(F^2 -1) ,

Answer 7

That is,

Answer 8

{2F^2 -2/F(2-F^2) dF

Answer 9

= {dx/x → (3)

Answer 10

The integrand on the left can be written as:

Answer 11

2F^2 -2/F(2-F^2)=A/F+B/√2+F+C/√2-F

Answer 12

Where the A,B,C are given from the system,

Answer 13

-A-B+C=2

Answer 14

B+C=0

Answer 15

& 2A= -2

Answer 16

Solving, we get

Answer 17

A=-1, B=-1/2 ,C=1/2

Answer 18

{2F^2 -2/F(2-F^2 dF= -{dF/F-1/2•{d(F+√2)/F+√2-1/2•{d(F-√2)/F-√2

Answer 19

=- lnF-1/2 ln(F+√2)-1/2 ln(F-√2

Answer 20

=- lnF-1/2 ln(F^2 -2)

Answer 21

=- lnF•√F^2 -2

Answer 22

And back in (3) we have

Answer 23

- ln F√F^2 -2

Answer 24

= lnx+c base 0

Answer 25

→ lnF√F^2 -2

Answer 26

= ln(1/ce^co)

Answer 27

→F^2•(F^2 -2)

Answer 28

=1/x^2 e^2co

Answer 29

Inverse transform:

Answer 30

(Y/x)^4 -2(y/x)^2

Answer 31

= 1/x^2 e^-2co→ y^4-2x^2 y^2 -cx^2=0

Answer 32

We get an incomplete quartic equation

Answer 33

This can be reduced to a quadratic

Answer 34

t^2 -2x^2•t-cx^2=0

Answer 35

With D=4x^2•(x^2+c)

Answer 36

t=x^2±x|√x^2+c|

Answer 37

t=y^2

Answer 38

± y=ab•sq•rt{x^2±x•ab•sq•rt^(x^2+c)}

Answer 39

Therefore,

Answer 40

Solve the homogeneous equation: y^3 dx+2(x^3-xy^2 )dy=0.

Divide through by y^3:

dx+2(x^3/y^3-x/y)dy=0

This is homogeneous in x/y, so let u=x/y or uy=x, and udy+ydu=dx. Therefore substitute for dx:

udy+ydu+2(u^3-u)dy=0=ydu+(2u^3-u)dy=0. 

ydu=(u-2u^3)dy; du/(u-2u^3)=dy/y; so ln|y|=∫du/(u-2u^3).

u-2u^3 factorises: u(1-2u^2)=u(1+u√2)(1-u√2) and break the integral into partial fractions:

A/u+B/(1+u√2)+C/(1-u√2)=(A(1-2u^2)+B(u-u^2√2)+C(u+u^2√2))/(u-2u^3)=1/(u-2u^3).

The only constant is A so A=1.

Equating coefficients:

u: B+C=0, so C=-B

u^2: -2A-B√2+C√2=0=-2A-B√2-B√2=0=-2-2B√2; 1+B√2=0, so B=-√2/2, and C=√2/2.

∫du/(u-2u^3)=∫du/u-(√2/2)∫du/(1+u√2)+(√2/2)∫du/(1-u√2)=

ln|u|-(1/2)ln|1+u√2|-(1/2)ln|1-u√2|=ln|(u/√(1-2u^2)|. [(1/2)ln|1+u√2|=ln(√(1+u√2)).]

We can include the constant of integration by writing ln|(Au/√(1-2u^2)|, where A is a constant, because the constant c can be replaced by A=ln(c).

So we have ln|y|=ln|(Au/√(1-2u^2)|; y=Au/√(1-2u^2), because the log arguments must be equal.

Finally we replace u by x/y:

y=A(x/y)/√(1-2x^2/y^2)=Ax/√(y^2-2x^2) (implicit equation).

This can be written as the quartic: y^4-2x^2y^2-A^2x^2=0.

[y^2=A^2x^2/(y^2-2x^2), y^4-2y^2x^2-A^2x^2=0=y^4-2y^2x^2+x^4-x^4-A^2x^2.

(y^2-x^2)^2=x^4+A^2x^2; y^2-x^2=±x√(x^2+A^2); y=x^2±x√(x^2+A^2); but it may be more appropriate to write x in terms of y: x^2=y^4/(2y^2+A^2) or x=±y^2/√(2y^2+A^2).]

If we want y in terms of x, this could be expressed as the solution of a quadratic:

y^2=x^2±x√(x^2+A^2), or graphed as a double parabola as shown in the graph below:

y^2-x^2±x√(x^2+A^2)=0 or y^4-2y^2x^2-A^2x^2=0. 

The graph appears to be something like (A has been given the arbitrary value 10 for the purpose of illustration):

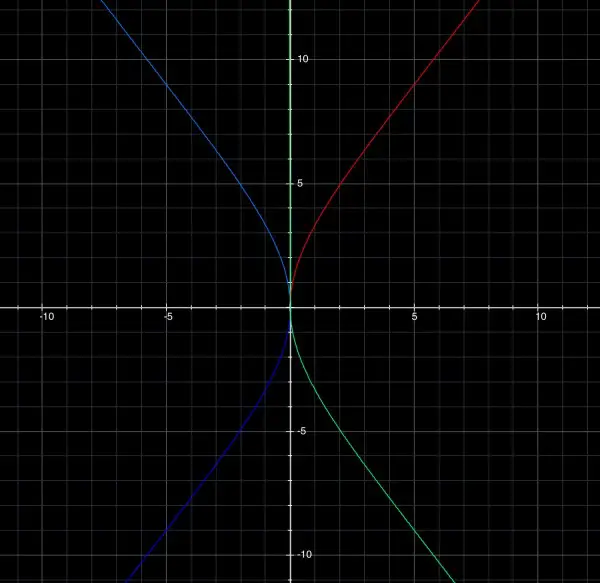
The various colours arise from ±. The graph is basically two horizontal parabolas touching at their vertices.

CHECK THE SOLUTION USING IMPLICIT DIFFERENTIATION

We arrived at the solution y=Ax/√(y^2-2x^2).

We can differentiate by using the identity d(u/v)/dx=(vu'-uv')/v^2, where u=Ax and v=√(y^2-2x^2).

So u'=A, v'=(2yy'-4x)/(2√(y^2-2x^2))=(yy'-2x)/√(y^2-2x^2).

Differentiating we get:

y'=(vu'-uv')/v^2=[A√(y^2-2x^2)-Ax(yy'-2x)/√(y^2-2x^2)]/(y^2-2x^2).

y'(y^2-2x^2)=[A(y^2-2x^2)-Ax(yy'-2x)]/√(y^2-2x^2)=A(y^2-2x^2-xyy'+2x^2)/√(y^2-2x^2)=A(y^2-xyy')/√(y^2-2x^2).

But y=Ax/√(y^2-2x^2), so A/√(y^2-2x^2)=y/x.

Therefore, y'(y^2-2x^2)=y(y^2-xyy')/x.

We need to find y' in terms of the other variables.

y'(xy^2-2x^3)=y^3-xy^2y'; y'(xy^2-2x^3+xy^2)=y^3=2y'(xy^2-x^3).

Rewriting y as dy/dx: y^3=2dy/dx(xy^2-x^3) or y^3dx+2(x^3-xy^2)dy=0, the original DE.

So the general solution, as an implicit equation, y=Ax/√(y^2-2x^2) is correct.