A general sine function would be y=asin(bx+c) where a, b and c are numerical constants.
a governs the amplitude, the distance between the x-axis and the peak or trough.
b governs the compression of the sine wave. The higher b is, the more peaks and troughs in a given interval.
c/b is based on the phase shift, displacement from the origin along the x-axis.
For y=sin(x), a=b=1, c=0 and the period is 2π (distance between two consecutive peaks or troughs). The amplitude=a=1.
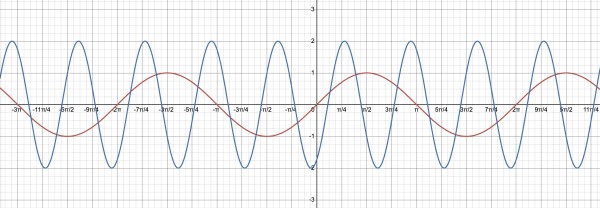
For y=2sin(3x-π/3), the amplitude=2, there are 3 peaks and 3 troughs in an interval of 2π. c=-π/3. The phase displacement from x=0 is π/9, because, when x=π/9, sin(3x-π/3)=sin(0)=0, a point on the x-axis.
The graph shows y=sin(x) in red and y=2sin(3x-π/3) in blue.
y=asin(bx+c)+d is the same graph as y=asin(bx+c) but is displaced d units vertically.