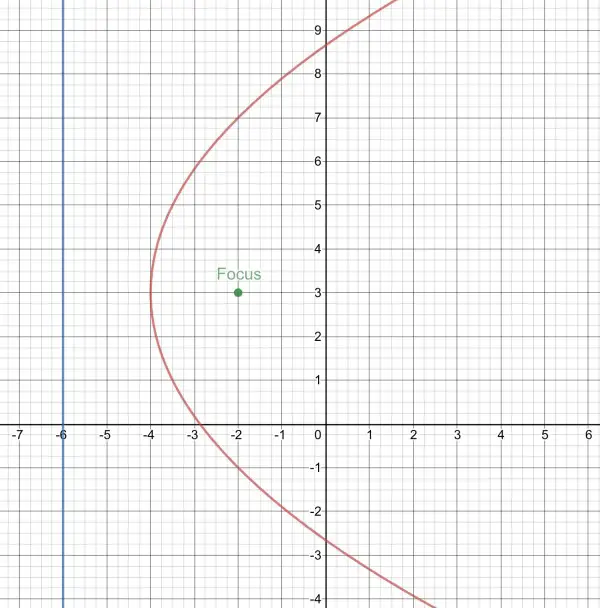
This is the description of a parabola, with directrix x+6=0 (x=-6) and focus (-2,3). The vertex lies midway on the perpendicular from the focus on to the directrix line. The midpoint is the average of the x coordinates -2 and -6, so x=-4 is the midpoint which must be on the perpendicular, so it has the same y coordinate as the focus, so the vertex is (-4,3). The parabola is resting on its side with arms pointing to the right:
x-(-4)=a(y-3)², x+4=a(y²-6y+9), or x/a+4/a=y²-6y+9. This can be written:
y²-x/a-6y+9-4/a=0.
From the given options, we must have y²-6y as part of the equation. The constant is -23=9-4/a, 4/a=32, a=⅛.
So -x/a=-8x, making the specific equation y²-8x-6y-23=0, answer a.