By plugging in the two points A and B into the equation of the circle we can confirm that they do indeed lie on the circumference of the circle and the line AB is a chord of the circle. The centre of the circle is at O(1,2), because this can be derived from the equation of the circle, being the displacements of the x and y coordinates.
There are an infinite number of diameters, so the question is incomplete. Let's assume that the required diameter has to be perpendicular to the chord AB. The midpoint of AB is M((4-1)/2,(5+4)/2)=M(1.5,4.5). The line OM is perpendicular to AB and its equation would be the diameter under this assumption. So we need the equation of the line passing through O(1,2) and M(1.5,4.5).
The gradient of the line OM is (4.5-2)/(1.5-1)=2.5/0.5=5.
The equation of OM and therefore of the assumed diameter is y-2=5(x-1), or we could use y-4.5=5(x-1.5).
This gives us y=5x-5+2=5x-3 or y=5x-7.5+4.5=5x-3 (red diameter).
So this particular diameter has the line equation y=5x-3.
If the assumption is wrong, that is, the diameter is not in fact perpendicular to the chord, then we're looking for something else that will give us just one unique diameter, for example, the diameter parallel to AB. In this case, the gradient of the diameter would be the gradient of AB (=-⅕) and the diameter would pass through O(1,2). The equation of the diameter would be:
y-2=-(x-1)/5, 5y-10=-x+1, 5y=11-x, y=⅕(11-x) (blue diameter).
So, you need to revise your question and see which (if any) of the above applies.
The general equation of the diameter would be y-2=m(x-1), y=mx-m+2, where m is an arbitrary gradient. Note that this does not involve either A or B, so the positions of A and B are significant in determining the equation of the diameter.
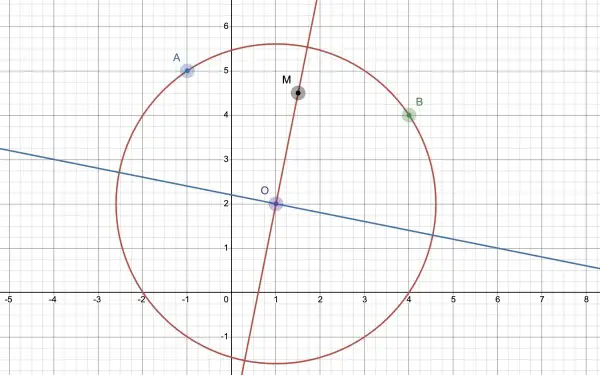
Two possible diameters shown in red and blue.