kx-1 =1⇒kx=2, k=2/x;
(k-2)x +ky=-2⇒(2/x-2)x+ky=-2, 2-2x+2y/x=-2, -x+y/x=-2, -x2+y=-2x, y=x2-2x;
(k²-1)z=9⇒(4/x2-1)z=9, 4z-x2z=9x2, z=9x2/(4-x2).
Here we have 4 unknown values: x, y, z, k, but only 3 equations. We need 4 equations to find the unknowns.
We have k, y and z in terms of x, so, knowing x will enable us to find k as well as y and z. We know that if x=±2, z would be indeterminate. And x=0 would make k indeterminate. If x=1:
k=2, y=-1 and z=3.
If x=-1, k=-2, y=z=3.
Other values of x would give other values for k.
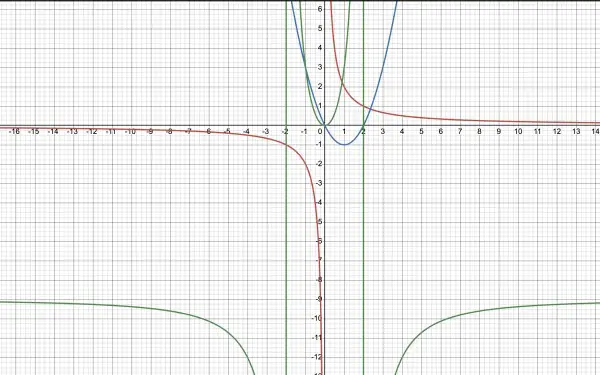
So k doesn't have a fixed value. In the graph below, the red curve represents the values that k can have, given x (on the horizontal axis). The blue curve is for y and the green curve for z. The two vertical green lines are not parts of the green graph, but are asymptotes for z. All the curves continue beyond the graphed area, so k can have any value, represented as a point, on the red curve. See for yourself the values of k, y and z when x=1 and -1. They are as calculated above. (The horizontal asymptote for z is at -9, and is not shown below.)
NOTE: If the third equation had been (k²-1)y=9, then substituting k=2/x in the other equations, we get:
y=x2-2x as before and (4/x2-1)(x2-2x)=9 (substituting for k and y)⇒x3-2x2+5x+8=(x+1)(x2-3x+8)=0.
The quadratic x2-3x+8=0 has no real solutions so x+1=0, x=-1 is the only real solution, from which k=-2 and y=3.
So the likely solution is k=-2, and there is an error in the question because "z" should have been "y" (or "y" should have been "z") and we would have had three equations and 3 unknowns.