linear programming with inequalitites

Question

A farmer wants to feed rabbits a mixture of two types of foods. Type I contains 8g of fat,
12g of carbohydrate and 2g of protein per unit, whereas Type II contains 12g of fat, 12g of
carbohydrate and 1g of protein per unit. Type I costs 20c per unit and Type II costs 30c per
unit. Each rabbit is to receive a daily minimum of 24g of fat, 36g of carbohydrate and 4g of
protein, but should get no more than 5 units of food per day.
(a) Express the feeding problem in terms of a system of constraint inequalities. (3)
(b) Give an objective function for the total cost. (1)
(c) Sketch the feasible region. (4)
(d) Determine the number of units of each type of food that should be fed to each rabbit
daily to satisfy the dietary requirement at minimum cost.

Answer 1

Type I feed: 8g fat + 12g carbohydrate + 2g protein (per 20c unit)

Type II feed: 12g fat + 12g carbohydrate + 1g protein (per 30c unit)

Let x=amount of Type I and y=amount of Type II in the mixture.

(a) Mixture constraints:

x+y≤5 (unit consumption)

8x+12y≥24 (fat consumption) simplifies to 2x+3y≥6

12x+12y≥36 (carbohydrate consumption) simplifies to x+y≥3

2x+y≥4 (protein consumption)

(b) Objective function: $z=0.20x+0.30y (to be minimised).

(c) The graph below represents the inequalities:

The shaded region on and to the left of the blue line represents x+y≤5.

The other lines represent the other inequalities and it's the regions to the right of each of these lines we are interested in. Both x and y must be positive (including zero); negative values have no meaning.

Green line: 2x+3y≥6; red line: x+y≥3; pink line: 2x+y≥4.

The lines intersect: green/pink (1.5,1); pink/red (1,2); green/red (3,0). All these points are within the blue region (x+y≤5). The red and blue lines are parallel. The only region satisfying all the inequalities is between x=3 and x=5. When x=3, y=2 (the point (3,2)). The triangular feasible region is bounded by (3,0), (3,2), (5,0).

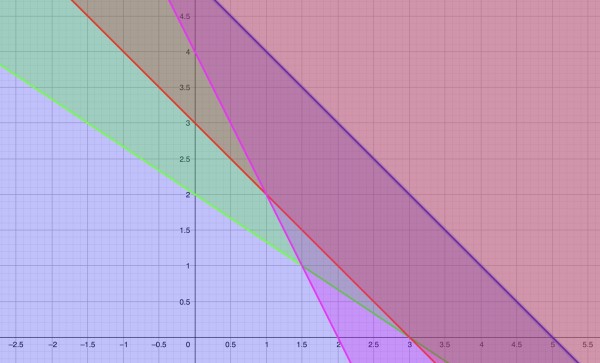
(d) If we plug these values into the objective function z=0.20x+0.30y, we get: z=$0.60 for (3,0), $1.20 for (3,2), and $1 for (5,0).

The minimum is z=$0.60, so that's 24g fat, 36g carbohydrate, 6g protein. These satisfy the constraints at minimum cost of 60c: 3 units of Type I feed and none of Type II.