(1-w)(1+w+w2)=1-w3. If 1-w3=0, w=1 is one root or zero and the other two zeroes are complex and can be represented geometrically by an Argand diagram, as you indicated, by three points on a circle on equal arcs. The points when joined form an equilateral triangle. The radii joining the points to the centre of the circle are at angles 0, 120°, 240° to the horizontal. The zero angle corresponds to (1,0) the real zero and the other two to the zeroes of 1+w+w2.
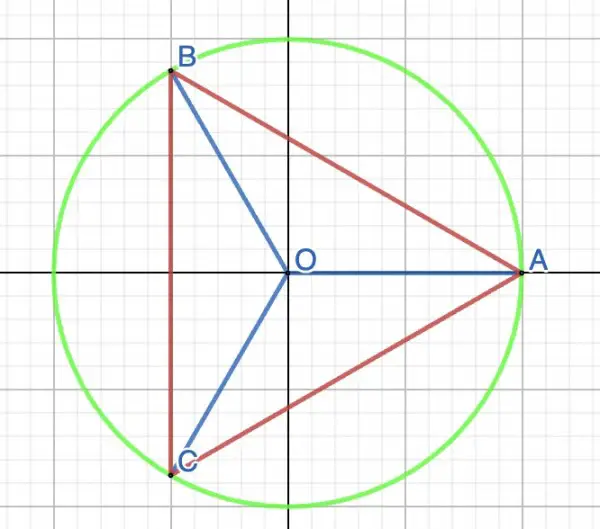
Points B(-½,½√3) and C(-½,-½√3) represent the complex zeroes w=-½+½i√3 and w=-½+½i√3, while A(1,0) represents the real zero, w=1. The blue radii represent the magnitude |w|=1 of each of the zeroes. The red equilateral triangle is just shown to indicate the symmetry of the zeroes, and the green circle just demonstrates that the zeroes are all on the circumference.
The quadratic formula, w=(-1±√(1-4))/2=-½±½i√3 confirms the graphical solution.