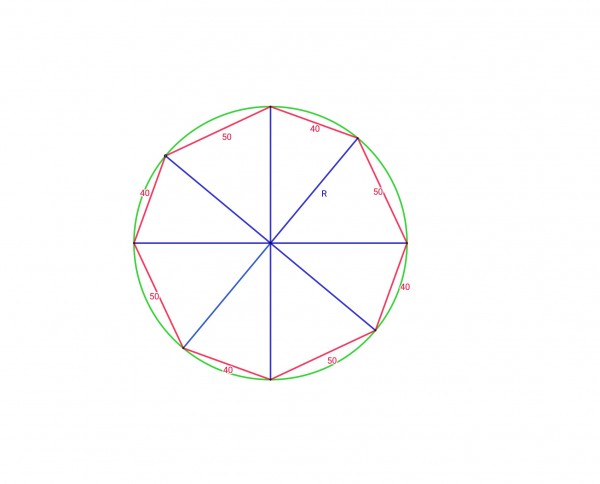
The picture shows the octagon drawn to scale inscribed in a circle. The eight angles at the centre must sum to 360°. There are also 8 isosceles triangles with the circle's radii making up their equal sides. If we call the smaller of the vertex angles of the triangles x and y, there are four of each of these so:
4x+4y=360 so x+y=90. Because of symmetry we only need to find the areas of the two triangles in one quadrant. One segment in the figure is shown with various labels: 40, 50 and radius R. To find x, we know that y=90-x. Each isosceles triangle can be split into two right angles with vertex angles x/2 and y/2 and bases 40/2=20 and 50/2=25. sin(x/2)=20/R, sin(y/2)=25/R, so sin(x/2)/sin(y/2)=20/25=4/5. But y=90-x so y/2=45-x/2 and sin(y/2)=sin45cos(x/2)-cos45sin(x/2).
sin45=cos45=1/√2. We have sin(x/2)√2/(cos(x/2)-sin(x/2))=4/5, 5sin(x/2)√2=4cos(x/2)-4sin(x/2), sin(x/2)(5√2+4)=4cos(x/2), tan(x/2)=4/(5√2+4), x/2=19.8649°, x=39.7298°, sin(x)=0.6392; and y=50.2702°, sin(y)=0.7691. (All figures approximate.)
R=20/sin(x/2)=58.8576.
The sum of the areas of the two triangles is ½R2sin(x)+½R2sin(y)=½R2(sin(x)+sin(y)).
The area of the octagon=4(½R2(sin(x)+sin(y)))=2R2(sin(x)+sin(y))=9756.85 square units.