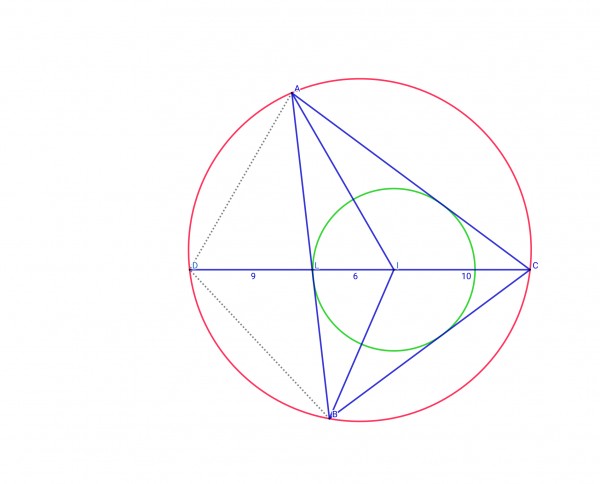
Join A to D and B to D to form ∆ABD. Let 2x=∠BAC, 2y=∠ABC. Note that the incircle plays no part in the solution.
∠BDC=2x, angles in the same segment BC. ∠ADC=2y, angles in the same segment AC. ∠ADB=2(x+y).
∠ACB=2(90-(x+y)), angles in ∆ABC sum to 180°.
In ∆ACD, ∠CAD=180-(90-x+y)=90+x-y, so ∠BAD=90+x-y-2x=90-(x+y).
In ∆BCD, ∠CBD=180-(90+x-y)=90-x+y, so ∠DBA=90-x+y-2y=90-(x+y).
So ∆ABD is isosceles, AD=BD. Using the sine rule in ∆ADL:
AL/sin(2y)=DL/sin(90-(x+y))=9/cos(x+y), so AL=9sin(2y)/cos(x+y). Using the sine rule in ∆AIL:
AL/sin(90-y)=IL/sin(x), AL/cos(y)=6/sin(x), AL=6cos(y)/sin(x).
Therefore, 6cos(y)/sin(x)=9sin(2y)/cos(x+y)=18sin(y)cos(y)/cos(x+y),
1/sin(x)=3sin(y)/cos(x+y), cos(x+y)=3sin(x)sin(y),
(cos(x)cos(y)-sin(x)sin(y)=3sin(x)sin(y),
tan(x)tan(y)=¼.)
Using the sine rule in ∆ADI:
AI/sin(2y)=DI/sin(90-x-y+x)=15/cos(y),
AI=15sin(2y)/cos(y)=30sin(y).
In ∆ACI, AI/cos(x+y)=CI/sin(x),
CI=30sin(x)sin(y)/cos(x+y)=30sin(x)sin(y)/3sin(x)sin(y)=10.
So CI=10cm.