Base of a regular triangular pyramid is an equilateral triangle. The three isosceles triangles forming the sides each have a base length of 4 and height 6.
The area of one of the isosceles triangles is ½(slant height)×base=½(6)(4)=12 square units. There are three isosceles triangles, so the lateral area is 36 square units.
The area of the equilateral triangle is ½(4²)sin(60°)=8(√3/2)=4√3. This is based on the formula for triangular area A=½bcsinθ where b and c are two sides including the angle θ. b=c=4 and θ=60°. (By splitting the equilateral triangle into two back-to-back right triangles of base 2 and hypotenuse 4, we can find the height = √(4²-2²)=√12=2√3, making the area A=½(4)(2√3)=4√3, which is the same value as ½(4²)sin(60°).)
The total surface area is 36+4√3 square units (about 42.93).
To find the volume we need the height H of the pyramid.
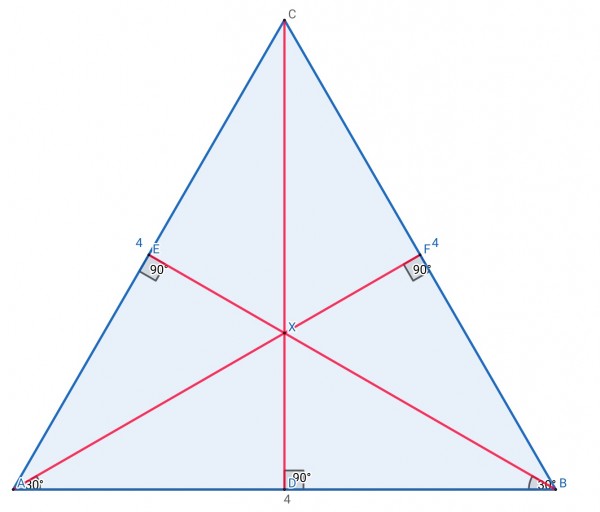
If we drop a perpendicular from the apex of the pyramid to the base, the length of the perpendicular will be H. The perpendicular meets the base at the centre of the equilateral base which is located where the medians intersect. This point is two-thirds the length of any median as measured from a vertex of the equilateral triangle.
The picture shows the base of the pyramid. The point X is where the medians intersect. The points D, E and F, being the midpoints of the base edges, are also points on the lateral surfaces from which the slant heights are calculated. Therefore, XD=XF=XE are the bases of the right triangles having height H. Since we know the slant heights, we can calculate H using Pythagoras’ Theorem:
H²+XD²=36, where XD/DB=tan(30°)=1/√3, and DB=2, XD=2/√3.
H²+4/3=36, H=√(36-4/3)=√(104/3)=2√(26/3).
The volume of the pyramid=⅓(base area)×H=⅓(4√3)(2√(26/3))=⅓8√26 cubic units (about 13.60).