Given: AE = 4 EB = 2 DE = 8 Find:EC

Question

Consider the following theorem.

If two chords intersect within a circle, then the product of the lengths of the segments (parts) of one chord is equal to the product of the lengths of the segments of the other chord.

O is the center of the circle.

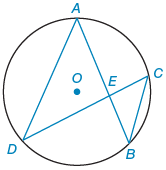A circle contains six labeled points and four line segments.

• The center of the circle is point O.
• Points A, B, C and D are on the circle. Point A is on the top middle, point B is on the bottom right, point C is slightly above the middle right, and point D is on the bottom left.
• A line segment connects points A and B.
• A line segment connects points C and D.
• A line segment connects points A and D.
• A line segment connects points C and B.
• Point E is the intersection of line segments A B and C D. Point E is to the right and slightly below point O.

Given:

AE = 4

EB = 2

DE = 8

Find:EC

Answer 1

Applying the theorem:

AE.EB=DE.EC,

4×2=8EC, so EC=8/8=1.