Segment One Honors Project

Question

Task 1 Part 1. Using the two functions listed below, insert numbers in place of the letters a, b, c, and d so that f(x) and g(x) are inverses.  f(x)= x+a b  g(x)=cx−d  Part 2. Show your work to prove that the inverse of f(x) is g(x).  Part 3. Show your work to evaluate g(f(x)).  Part 4. Graph your two functions on a coordinate plane. Include a table of values for each function. Include 5 values for each function. Graph the line y = x on the same graph.  Task 2 Part 1. Create two radical equations: one that has an extraneous solution, and one that does not have an extraneous solution. Use the equation below as a model.  a√x+b+c=d  Use a constant in place of each variable a, b, c, and d. You can use positive and negative constants in your equation.  Part 2. Show your work in solving the equation. Include the work to check your solution and show that your solution is extraneous.  Part 3. Explain why the first equation has an extraneous solution and the second does not.  Task 3 Part 1: Create a scenario for an arithmetic sequence. For example, Jasmine practices the piano for ______ minutes on Monday. Every day she ___________ her practice time by _________. If she continues this pattern, how many minutes will she practice on the 7th day? Be sure to fill in the blanks with the words that will create an arithmetic sequence. Use your scenario to write the function for the 7th term in your sequence using sequence notation.  Part 2: Create a scenario for a geometric sequence. For example, Anthony goes to the gym for ______ minutes on Monday. Every day he _________his gym time by ____________. If he continues this pattern, how many minutes will he spend at the gym on the 5th day? Be sure to fill in the blanks with the words that will create a geometric sequence. Use your scenario to write the formula for the 5th term in your sequence using sequence notation.  Part 3: Use your scenario from part 2 to write a question that will lead to using the geometric series formula. Use the formula to solve for Sn in your scenario.

Answer 1

TASK 1, parts 1-3

Let y=f(x)=x+ab, then x=y-ab. If x=g(y)=y-ab, so g(x)=x-ab.

But were given g(x)=cx-d, therefore cx-d≡x-ab. If we equate coefficients, c=1 and d=ab. Let a=2 and b=-3, then d=-6. f(x)=x-6, g(x)=x+6.

f(g(x))=x and g(f(x))=x if f and g are mutual inverses, so:

f(g(x))=f(x+6)=(x+6)-6=x and g(f(x))=g(x-6)=(x-6)+6=x, confirming mutual inverses.

Part 4

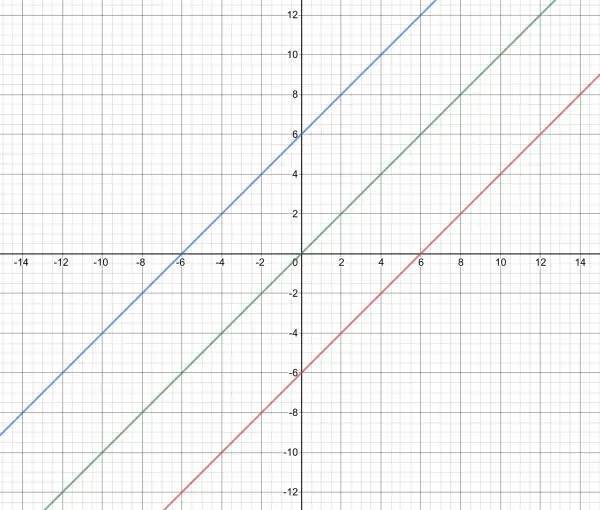
  x  f(x)  g(x)

-6   -12     0

-3   -9       3

 0   -6       6

 3   -3       9

 6    0      12

f(x) is red, g(x) is blue and y=x is green.

TASK 2

Part 1

2√(x+1)+7=5 is a radical equation with an extraneous solution.

Part 2

2√(x+1)+7=5, 2√(x+1)=-2, √(x+1)=-1, square both sides: x+1=1, x=0.

But 2√(x+1)+7=9 when x=0 and 9≠5. So x=0 is an extraneous solution.

2√(x+1)+5=7 is a radical equation with solution x=0.

Part 3

The extraneous solution is a result of squaring because (-1)²=1²=1. This creates an ambiguity. But √(x+1) specifically implies the positive root. This is the reason why the second equation works, because the positive root satisfies the equation.

TASK 3

Part 1

“Jasmine practises the piano for thirty minutes on Monday. Every day she increases her practice time by five minutes...”

f(n)=30+5(n-1) where n is the number of days after Monday, and f(n) is practice time. As an AP, a_n=30+5(n-1), or a₁=30 and a_(n+1)=a_n+5.

7th term (n=7), a₇=30+5×6=60 minutes.

 

Parts 2 and 3

“Anthony goes to the gym for fifty minutes on Monday. Every day he increases his gym time by eight percent...”

g(n)=50×1.08ⁿ⁻¹ where n is the number of days after Monday, and g(n) is gym time. As a GP, term T_n=50(1.08)ⁿ⁻¹, or T₁=50 and T_(n+1)=1.08T_n. 5th term (n=5), T₅=50(1.08)⁵=73.47 minutes (approx).

“If I go to the gym for 50 minutes on Monday and decide to increase my gym time by 8% for each subsequent day thereafter, by how many minutes will my gym time have increased by Saturday? (Accurate to 1 decimal place.)” Answer: 73.47-50=23.47, that is, 23.5 minutes increase.