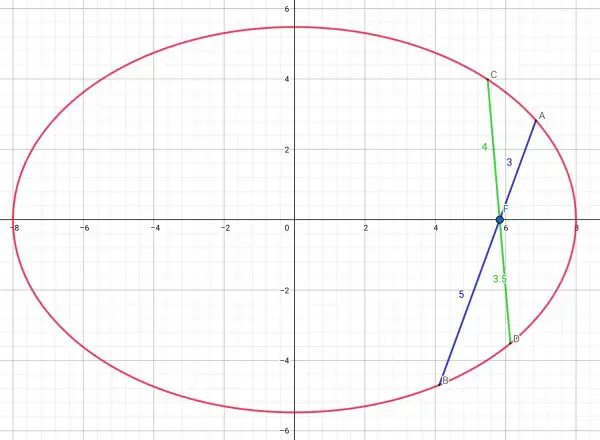
Equation of ellipse: x²/a²+y²/b²=1.
If F(c,0) is a focus, where c²=a²-b², then
x²/a²+y²/(a²-c²)=1, y²=(a²-c²)(1-x²/a²).
Circle centre F, radius=p:
(x-c)²+y²=p².
When the circle intersects the ellipse, we have:
(x-c)²+(a²-c²)(1-x²/a²)=p²,
x²-2cx+c²+a²-x²-c²+c²x²/a²=p²,
-2cx+a²+c²x²/a²=p²,
c²x²-2a²cx+a⁴-a²p²=0.
x=(2a²c±√(4a⁴c²-4c²(a⁴-a²p²))/(2c²),
x=(2a²c±√(4a²c²p²))/(2c²),
x=(2a²c±2acp)/2c²=(a²±ap)/c.
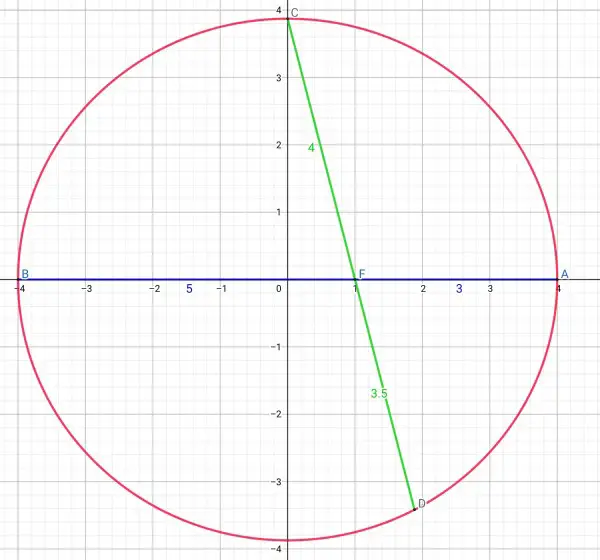
To find the x coordinate of A, circle C₁ radius p=AF=3, x=(a²±3a)/c.
Similarly the x coordinate of B, circle C₂ radius p=BF=5, x=(a²±5a)/c.
The cosine of the inclination of AF (and therefore AB) is (x-c)/3=((a²±3a)/c-c)/3, when x>c, and of BF is (c-(a²±5a)/c)/5 (x<c). When these two cosines are equal (AB is a chord):
((a²±3a)/c-c)/3=(c-(a²±5a)/c)/5,
(5a²±15a)/c-5c=(3c-3a²∓15a)/c,
(8a²+15a(±1±1))/c-8c=0,
(8a²+15a(±1±1))-8c²=0,
8(a²-c²)+15a(±1±1)=8b²+15a(±1±1)=0, because a²-c²=b² by definition.
So 8b²=-15a(±1±1). The only feasible solution is 8b²=-15a(-2)=30a, b²=15a/4.
So the equation of the ellipse is:
x²/a²+4y²/15a=1. Also, c²=a²-15a/4=a(a-3.75).
That means a>3.75. (The circle must be large enough to intersect the ellipse.)
The cosine of the inclination of CF is ((a²±4a)/c-c)/4 and of DF (unknown) is (c-a²±pa)/c)/p, because the x coordinates of C and D must be on either side of the focus.
Since these must be equal:
((a²±4a)/c-c)/4=(c-(a²±pa)/c)/p.
(pa²±4pa)/c-pc=4c-(4a²±4pa)/c,
((p+4)a²+4pa(±1±1)-(p+4)c²=0,
(p+4)b²+4pa(-2)=0,
b²p+4b²=8pa,
4b²=p(8a-b²)
p=4b²/(8a-b²)=15a/(8a-3.75a)=15/4.25=60/17, substituting b²=15a/4.
Therefore DF=60/17=3.5294 approx. does not depend on the shape of the ellipse.