Finding coordinates of vertices

Question

x ≥ 0

 y ≥ 0

x ≤ 10

 x + y ≥ 5

 x + 2y ≤ 18

1. Find the coordinates of the vertices of the feasible region. Show how you found them

Answer 1

First, a picture:

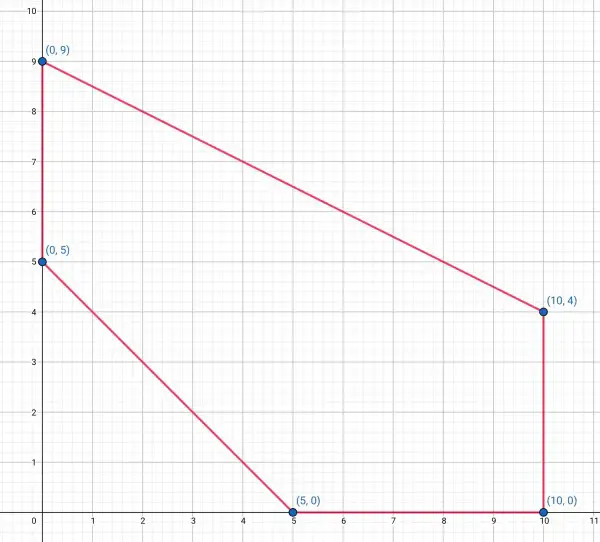
x and y are both positive so all vertices are in the first quadrant.

So we find the leftmost coordinates first. This is when x=0, so we can plug x=0 into the lines x+y=5, y=5 and we have the point (0,5). And for x+2y=18 we get y=18/2=9, the point (0,9).

Moving further to the right we have an extreme of x=10. Plug x=10 into the two lines, 10+y=5 gives us y=-5 so that point is outside the region. It’s superseded by the condition y=0 which gives x=5 and the point (5,0). Plug x=10 into the other equation: 10+2y=18, 2y=8, y=4. So the x and y values are in the region giving the point (10,4). x cannot exceed 10 and y cannot be negative, so the point (10,0) is another vertex. The region has to be above the line x+y=5 and below x+2y=18. The 5 vertices are therefore: (0,5), (0,9), (5,0), (10,4), (10,0), a pentagon.