Positive integers

Question

We say that a positive integer is quiteprime if it is not divisible by 2, 3, or 5. How many quiteprime positive integers are there less than 100? less than 1000? A positive integer is very quiteprime if it is not divisible by any prime less than 15. How many very quiteprime positive integers are there less than 90000? Without giving an exact answer, can you say approximately how many very quiteprime positive integers are less than 1010? less than 10100? Explain your reasoning as carefully as you can.

Answer 1

I’m treating actual primes as quiteprimes for this exercise. So 1, 2, 3, 5 would be quiteprimes.

Define some sets for [1,99]:

S2[1,99]={2 4 6 ... 98}, S3[1,99]={3 6 9 ... 99}, S5[1,99]={5 10 15 ... 95}.

Also designate n(S) as the size of set S, so:

n(S2[1,99])=49, n(S3[1,99])=33, n(S5[1,99])=19, since 98/2=49, 99/3=33, 95/5=19.

We can find how many “composites” there are by applying the intersection of two sets S₁ and S₂:

n(S₁&S₂)=n(S₁)+n(S₂)-n(S₁∩S₂). This means we add the size of the sets and subtract the number of elements they have in common.

So combining numbers divisible by 2 and 3 we have S6[1,99]={6 12 18 ... 96}. These elements appear in the sets for both 2 and 3. There are 16 of these, so the total composites for 2 and 3 are 49+33-16=66.

Call this n(S2&S3[1,99])=66.

Now we need to consider S5.

n(S2&S3&S5[1,99])=66+19-n(S2&S3[1,99]∩S5[1,99]).

Let’s see what S2&S3[1,99] looks like:

{2 4 6 8 10 12 ... 98} ∪

{3 6 9 12 15 18 ... 99}={2 3 4 6 8 9 10 12 14 15 16 18 ... 98 99} (66 elements)

S10[1,99]={10 20 ... 90}, n(S10[1,99])=9 (2×5=10)

S15[1,99]={15 30 ... 90}, n(S15[1,99])=6 (3×5=15)

S10[1,99]∪S15[1,99]={10 15 20 30 40 45 50 60 70 75 80 90}, n(S10[1,99]&S15[1,99])=12

S30[1,99]={30 60 90}, n(S30[1,99])=3 (2×3×5) are already accounted for in n(S10[1,99]&S15[1,99]).

Combining the three sets above also gives us 12: 9+6-3=12.

So we now combine the 66 elements identified earlier (from the union of 2 and 3 divisible); n(S5[1,99])=19.

66+19=85, but we have to subtract the 12 resulting from combining S15[1,99] and S10[1,99]:

85-12=73. So if we subtract this from the 99 integers (1-99) we get 26 which are are quiteprime.

The 73 composites include 2, 3 and 5. So by the assumption that, because they’re actual primes, we need to add them to the list of quiteprimes and subtract them from the composites. That gives us 29 quiteprimes.

The table below shows actual designations as composites and quiteprimes.

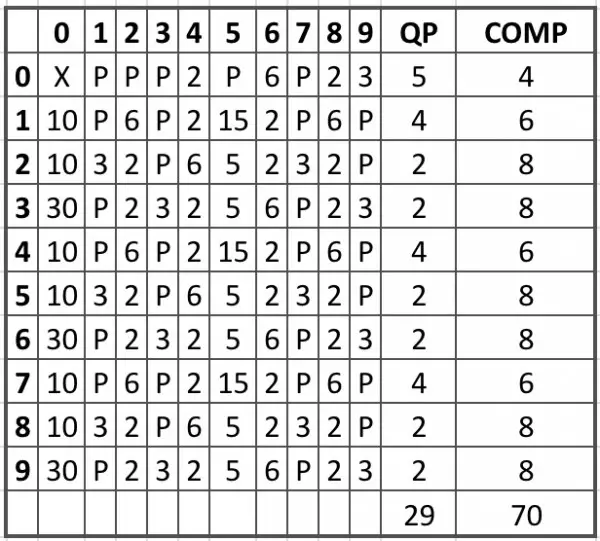
More to follow...

 

(WARNING: There is a physical limit of 12,000 characters for an answer on this website, so it may not be possible to give comprehensive answers.)

Comments

Would you please leave it on the comment section if the space isn't enough? Thanks!

---

I was rather hoping you would have enough clues from my answer to allow you to continue looking at the problem for yourself. I’m still working on this question (which I do find very interesting) but I only have a limited time to spend (I’m only an ordinary user like yourself) and other users are equally entitled to have their questions answered, too! It may take me a few days to structure the answer concisely, but I’ll cram as much into the answer section as I can, and use the comments for overspill. I should also tell you that I have particular difficulties editing, especially as an answer gets longer. The system becomes very slow and unresponsive and several times I have lost answers because the system has refreshed or reloaded while I’m  still answering a question—perhaps because I’m not located in the US, so network performance may not be so good. So please be patient!