We need to find the volume V by converting rectangular ∫∫zdydx over region R to polar ∫∫zrdrdθ, by rewriting z in terms of r and θ instead of x and y. So, since the surface z is defined as z=√(x²+y²), and x²+y²=r², z=r is the polar equation of the cone.
R is the area of the given circle x²+y²=4, so r²=4 and r=2.
We can now work out the limits for R: the whole circle gives the limits for θ as [0,2π], while the limits for r are [0,2], so the double integral becomes:
V=∫∫r²drdθ with the aforementioned limits.
This evaluates to ∫[⅓r³]dθ=∫(8/3)dθ=(8/3)[θ]=(8/3)2π=16π/3 cubic units.
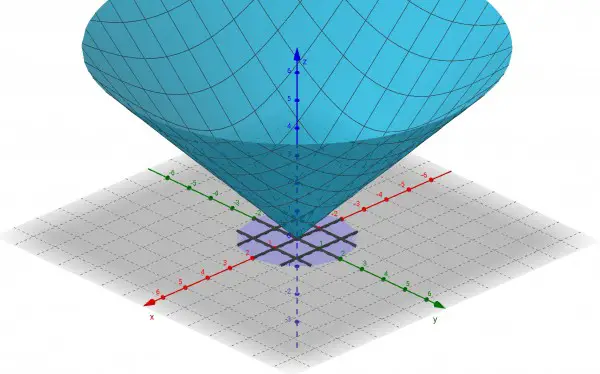
This can be confirmed geometrically. A cylindrical block with radius 2 and height 2 has a conical volume, with the same radius and height, drilled out of it. V is the difference in volume of the two figures: πr²h-⅓πr²h=⅔πr²h, where h=r=2. This evaluates to 16π/3 as the volume of material left in the block.
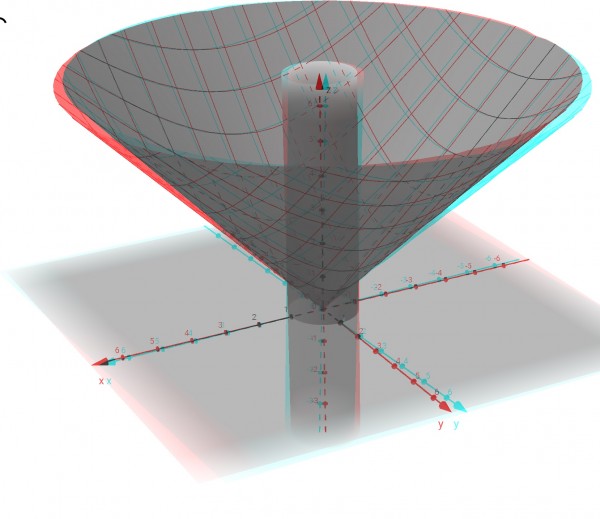
The picture can also be viewed in 3D using a 3D viewer with filters: green/blue for the right eye and red for the left eye. The purple circle, representing R, can be extruded into a cylinder embracing the cone and cutting it off when the base of the right circular cone (top surface) has the same area as R.