Above is the revised picture.
It’s different because you gave A(0,2) as the point, when it probably should have been A(0,-2). If you make the necessary changes in the solution you should get the answer in your textbook.
Feel free to send me a private message if you still need help. In the meantime I can revise my solution on the assumption that A is the point (0,-2).
REVISED SOLUTION
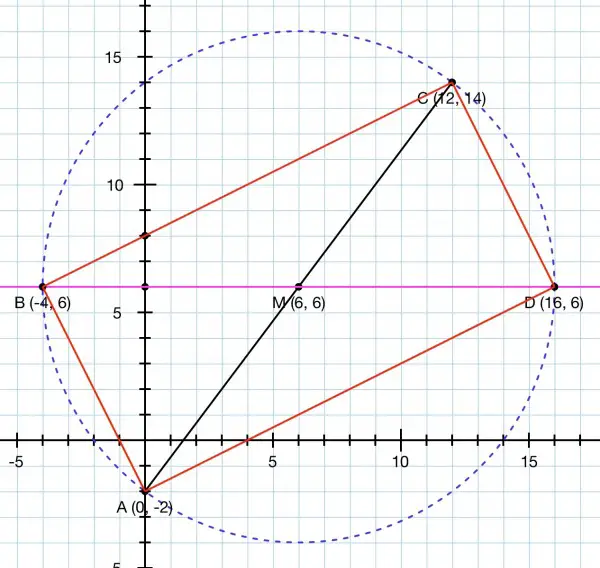
The diagonals of a rectangle bisect one another, so first we find the midpoint M of diagonal AC, which is the average of the endpoints: ((0+12)/2,(-2+14)/2)=M(6,6). Since diagonal BD passes through M and is parallel to the x-axis, it must have a y coord of 6, since the horizontal line has the equation y=6.
We have the centre of a circle M and radius MC so we can draw a circle passing through A and C, with AC (or BD) as diameter. Any point P on the circumference forms a right angle APC, because the angle subtended by a diameter is a right angle, so the positions of B and D are determined by the intersection of y=6 with the circle.
Using Pythagoras’ Theorem we can work out the radius of the circle=√((6-(-2))²+(6-0)²)=√(8²+6²)=√100=10. The equation of the circle is (x-6)²+(y-6)²=100. When y=6, x-6=±10, which gives us the x coords of B and D.
B(6-10,8) and D(6+10,8)=B(-4,8) and D(16,8). So h=16.
The gradients of AD (or BC) and CD (or BA) are (6-(-2))/(16-0)=½ and (6-(-2))/(-4-0)=-2. So we have the gradients as 8/h and -h/8. The product of the gradients of two lines perpendicular to one another is -1, and ½×(-2)=-1, and AD and CD are perpendicular to each other.
Note that 8/(12-h)=8/(-4)=-2=-h/8 when h=16.