UAs far as I can discover, there is no function of x equivalent to this integral.
However, various approximation methods can be used. We can make use of the regular zeroes of the integrand function and also the symmetry (it’s an even function) to work out expressions of an infinite series.
The zeroes start at t=√(2π-4) and, for integer n>1 we can use definite integration for finding a good approximation of the areas under the curve (or between the curve and the t axis) between the zeroes at t=√(nπ-4), √((n+½)π-4). These give us right triangles (approx) the areas of which can be summed. The curve oscillates between +1 and -1. A first approximation would be to sum the areas of the right triangles with a height of 1. This is what integration does but to an infinitesimal degree. The triangles get narrower as n increases. They appear alternately above and below the axis, so the net area is the difference between the area above and the area below. A special case is between t=0 and t=√(2π-4) where the curve is below the axis so has a negative value. You could use the Riemann sum here.
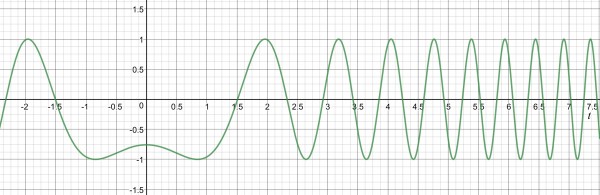
The definite integral of the function appears to converge to about -0.88 as n increases to infinity. So for the whole range (-∞,∞) the integral converges to a value of about -1.76 because of symmetry.