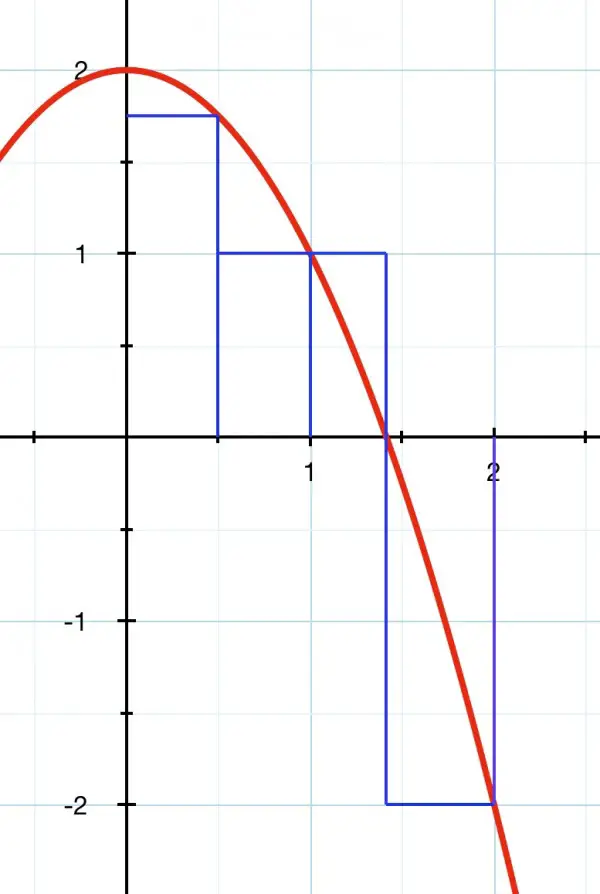
GgThe idea of the Riemann sum is to find the area under a curve between the curve and (usually) the x-axis by dividing a given interval into rectangles, then summing the areas of the rectangles. In this case the rectangles will be half a unit wide because the interval 0 to 2 is split into 4. We can use the rectangle whose top left hand vertex touches the curve (giving the rectangle’s length) or we can use the right hand top vertex, which is what we are asked to use in this case.
f(0)=2, f(0.5)=1.75, f(1)=1, f(1.5)=-0.25, f(2)=-2.
Note that f(1.5) and f(2) are negative, which means the curve goes under the x-axis. We have to be careful now, because we don’t have a complete rectangle between f(1) and f(1.5). When f(x)=0 x=√2. If we want the areas of the rectangles to be summed no whether the curve is above or below the x-axis, then we need to split the interval from x=1 to 1.5 into [1,√2] and [√2,1.5]. The alternative is to vary the width of two rectangles so that one is entirely above the x-axis and one entirely below. The latter is probably the better alternative, so we’ll use it. We know that f(√2)=0 and it doesn’t matter that the widths of the rectangles differ.
The lengths and widths of the chosen rectangles are (length,width)=
(f(0.5),0.5), (f(1),0.5), (f(√2),√2-1), (-f(2),2-√2).
The four areas added together are:
1.75×0.5+1.0×0.5+1.0×(√2-1)+2.0×(2-√2)=
0.875+0.5+0.414+1.172=2.961. The picture below should make things clearer. The parabolic curve is in red with the outline of the rectangles in blue. Note that if integration were to be used, the area below the x-axis would be subtracted from the area above. I have added it as 1.172 so that a true approximate area is evaluated.