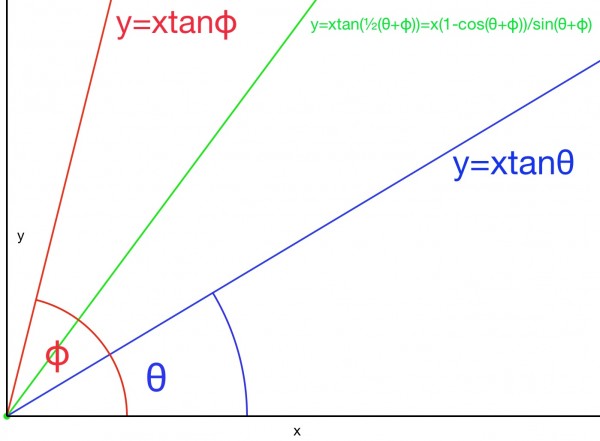
The picture shows three lines and the green line bisects the angle between the red and blue lines. The gradients are shown as the tangents of the angles each line makes with the x axis. The angle of the green line is the average of the other two angles. The trig identity shows that the tangent of this average can be expressed in terms of the sum of the angles of the red and blue lines.
The equations of the lines can be written:
y-px=0, y-qx=0, y-rx=0 where p=tanθ, q=tanɸ, and we will calculate r in terms of p and q later. We can combine the three equations into one:
(y-px)(y-qx)(y-rx)=0=y³-xy²(p+q+r)+x²y(pq+pr+qr)-pqrx³.
We can also rewrite the given cubic: y³-(c/d)xy²+(b/c)x²y-(a/d)x³=0. And we can relate p, q and r to a, b, c and d. First, we need to find r in terms of p and q.
Since tanθ=p, sinθ=p/√(1+p²), cosθ=1/√(1+p²), and since tanɸ=q, sinɸ=q/√(1+q²), cosɸ=1/√(1+q²).
r=(√((1+p²)(1+q²))+pq-1)/(p+q).
We are now in a position to start matching coefficients of the cubic.
p+q+r=-(c/d), pq+pr+qr=(b/d), pqr=-(a/d).
What follows is an indicative proof by substituting numbers for the letters.
From observation, we can find integer values for (p,q,r)=(1,7,2).
From these values we can find a, b, c, d:
-a/d=14, b/d=23, -c/d=10. If we put d=1, the cubic looks like:
-14x³+23x²y-10xy²+y³=0.
Substituting these values for a, b, c, d into the given equation for proof:
(-42-10)²(-230-20+42)=(-52)²(-208)=562432
(23+3)²(-230-644+42)=(26)²(-832)=562432
So the equation is satisfied.
Changes in the site software, difficulty in editing, and limitations of text size hinder a more expansive, algebraic proof. If a shorter, concise proof is forthcoming, I will replace or supplement this solution.