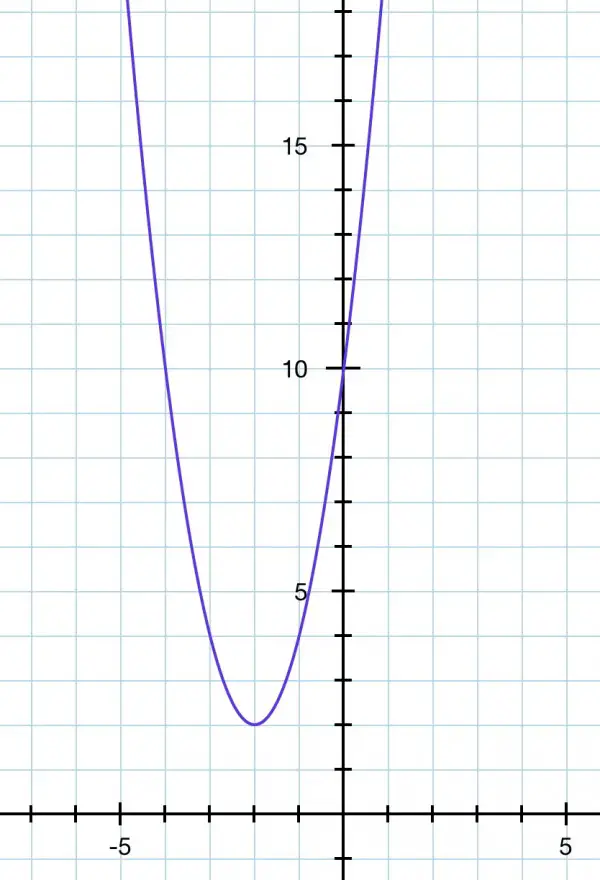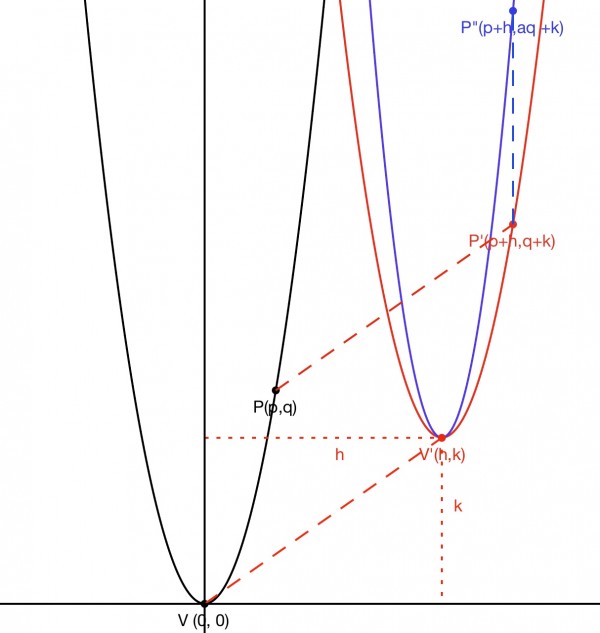
The graph shows the transformation process from the parent function (the black parabola).
I’ve considered a general transformation in which the parabola is shifted horizontally and vertically and a dilation factor introduced. Later we can put in explicit values for these general values.
First transformation: the red parabola is created by shifting the parent h units to the right and k units up. The vertex at the origin V(0,0) is moved to V'(h,k) and the movement is indicated by the red dashed line. We can reverse the movement: a negative value for h would move the parent to the left and a negative value for k would move the parent down. If we take a point P(p,q) it is moved to P'(p+h,q+k) so that the relative position with the vertex stays the same. So y-k=(x-h)² or y=f(x)=(x-h)²+k.
Second transformation: the blue parabola is created by applying the dilation factor to the y-coord, without affecting the x-coord or the position of the vertex. So y-k=a(x-h)² or y=f(x)=a(x-h)²+k where a is the dilation factor.
In the given function, a=2, h=-2, k=2. So the 1st transformation moves the parent y=x² 2 units to the left and 2 units up. The dilation factor narrows the parabola so that the vertical displacement from the vertex is doubled.