cos(x-y)-cos(x+y)=2sin(x)sin(y)prove the identities with each step

Question

prove the identity with showing steps and telling each identity

Answer 1

cos(x-y)=cosxcosy+sinxsiny

cos(x+y)=cosxcosy-sinxsiny

Add: cos(x-y)-cos(x+y)=2sinxsiny.

To prove the identities:

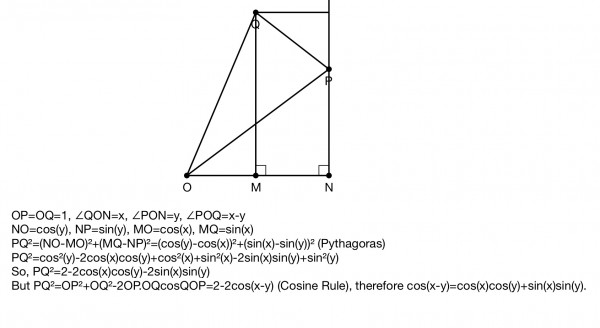
OP=OQ=1, ∠QON=x, ∠PON=y, ∠POQ=x-y

NO=cos(y), NP=sin(y), MO=cos(x), MQ=sin(x)

PQ²=(NO-MO)²+(MQ-NP)²=(cos(y)-cos(x))²+(sin(x)-sin(y))² (Pythagoras)

PQ²=cos²(y)-2cos(x)cos(y)+cos²(x)+sin²(x)-2sin(x)sin(y)+sin²(y)

So, PQ²=2-2cos(x)cos(y)-2sin(x)sin(y)

But PQ²=OP²+OQ²-2OP.OQcosPOQ=2-2cos(x-y) (Cosine Rule), therefore cos(x-y)=cos(x)cos(y)+sin(x)sin(y) when we equate the two expressions for PQ².

To find cos(x+y) substitute -y for y:

cos(x+y)=cos(x)cos(y)-sin(x)sin(y) because cos(-y)=cos(y) and sin(-y)=-sin(y).