The As the pipe is raised, its vertical height y and horizontal position x are related by Pythagoras’ Theorem:
x²+y²=40². So y²=40²-x², and 2ydy/dt=-2xdx/dt, that is, ydy/dt=-xdx/dt, where t is time.
dy/dt is rate of increase in the vertical height of the end of the pipe, while -dx/dt is the rate of horizontal decrease in the free end of the pipe as it moves towards an upright position. It starts 40 feet away from its upright position and ends zero feet from upright.
The winch pulls in the rope so the length of rope decreases at the constant rate of 0.5 ft/sec, and the end of the pipe rises at the rate of 0.5 ft/sec, so dy/dt=0.5. The rate of vertical change is 0.5 feet per second.
So, 0.5y=-xdx/dt. When y=20 feet, -xdx/dt=10. Also, when y=20, x=√(1600-400)=20√3 feet.
The rate of horizontal change is dx/dt=-10/(20√3)=-√3/6=-0.29 ft/s approx.
This means that when half the rope has been winched in, so that the end of the pipe is 20 feet above the ground, and the free end has moved from 40 ft to 20√3=34.64 feet, a distance of 5.36 ft from its starting position, the tied end is moving vertically at 0.5 ft/s while the free end is decreasing at a rate of 0.29 ft/s as it swings towards the building.
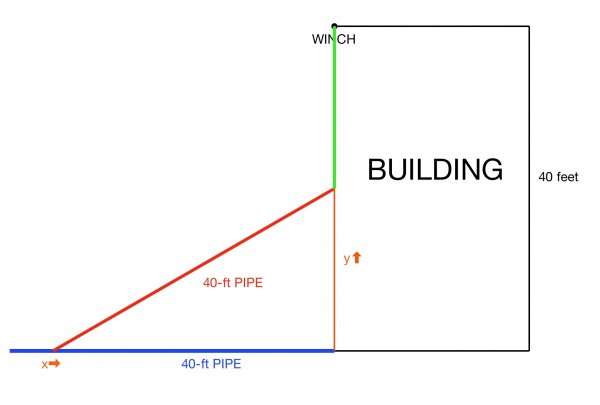
Starting position of the pipe is shown in blue and in red when it has been raised to its halfway position. Green represents the length of rope from the winch.