If the equation of the circle is (x-h)²+(y-k)²=9 where (h,k) is the centre, we can find the gradient by differentiation: 2(x-h)+2(y-k)(dy/dx)=0. At (1,2) the gradient dy/dx is given by 1-h+(2-k)(dy/dx)=0.
Therefore dy/dx=(h-1)/(2-k). Point (1,2) lies on the circle: (1-h)²+(2-k)²=9.
The gradient of the line 5x-2y-1=0 is given by dy/dx: 5-2(dy/dx)=0, dy/dx=5/2. This gradient is tangent to the circle, so (h-1)/(2-k)=5/2, 2h-2=10-5k, 2h=12-5k, h=6-5k/2.
So, (1-6+5k/2)²+(2-k)²=9,
25(k/2-1)²+4-4k+k²-9=0,
25(k²/4-k+1)-5-4k+k²=0,
25k²/4-25k+25-5-4k+k²=0, 29k²/4-29k+20=0.
(29/4)(k²-4k)=-20, (29/4)(k²-4k+4-4)=-20, (29/4)((k-2)²-4)=-20, (29/4)(k-2)²-29=-20, (k-2)²=36/29.
k-2=±6/√29, k=2±6/√29, h=6-(5/2)(2±6/√29)=6-5∓15/√29=1∓15/√29.
So we have two circles with different centres: (1-15/√29,2+6/√29) and (1+15/√29,2-6/√29).
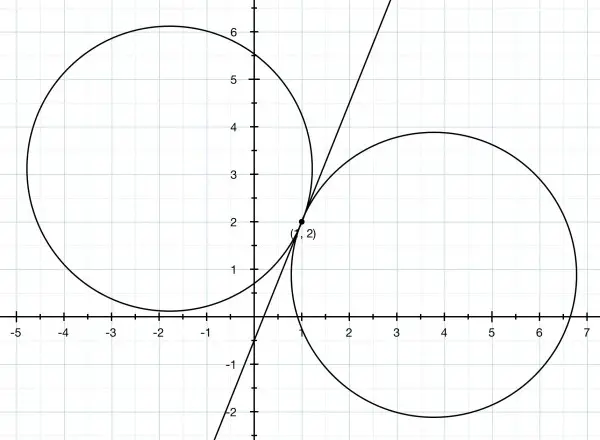
The graph shows the two circles and their common tangent drawn to scale.