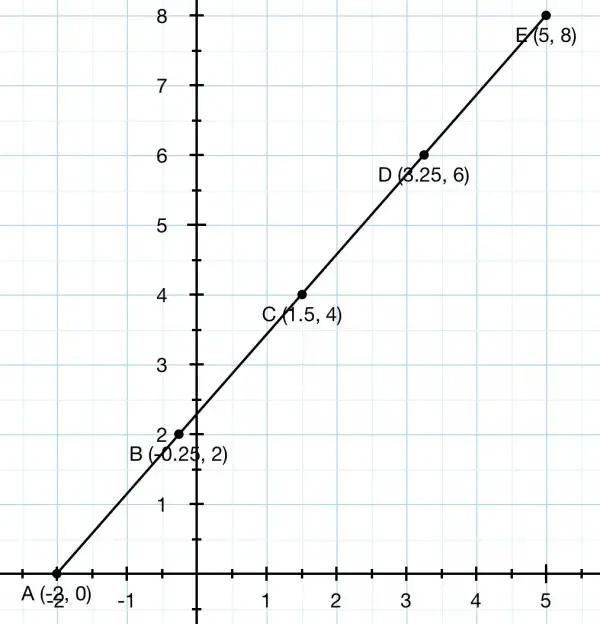
Label these points A(-2,0) and E(5,8).
Find the mid point C first by averaging the x and y coords:
x=(5-2)/2=3/2=1.5; y=(8+0)/2=4. So the midpoint is C(1.5,4).
Now find the midpoint of the two half segments: x=(5+1.5)/2=6.5/2=3.25; y=(8+4)/2=6; D(3.25,6) is one point.
x=(1.5-2)/2=-0.25; y=(4+0)/2=2; the other point is B(-0.25,2).
We now have points A, B, C, D, E, and 4 segments: AB, BC, CD, DE spaced equally along segment AE.
What we have is A...B...C...D...E. BE=3AB, so BE/AB=3 that is, BE:AB=3:1. And we have AD=3DE so AD/DE=3 that is, AD:DE=3:1.
Therefore to divide the segment AE into two segments AB and BE we just have to use the coords of B(-0.25,2) or D(3.25,6). I think that, because the segment is directed from A to E, the point B is the correct answer: (-0.25,2) and this is the “1” in the ratio AB:BE=1:3. AB is a quarter the way along AE.
A picture will make this clearer: