First, write both equations so that we have y=...
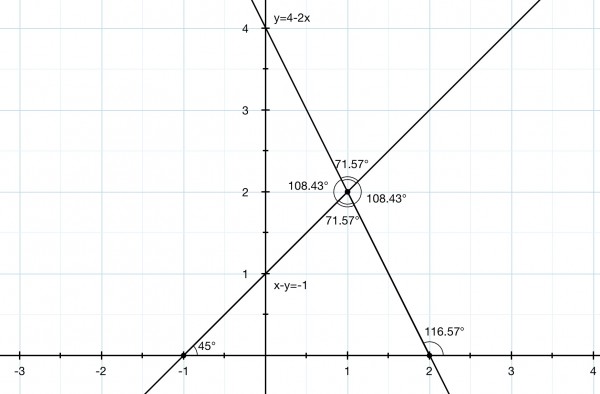
y=4-2x
y=x+1, by rearrangement.
We can equate these to find x: 4-2x=x+1, 3=3x, so x=1. Therefore y=x+1=1+1=2.
So the point of intersection is (1,2).
To find the angle between them we need the slopes which are the x coefficients of the 2 equations after rearrangement: -2 and 1. These are the tangents of the angles of slope so we can work out what the angles are. When the slope is negative the angle is obtuse (between 90 and 180 degrees). In this case we find the angle whose tangent is the positive equivalent of the slope (2 in this case), so we get 63.43°. And we find its supplement 180-63.43=116.57°. When the slope is positive the angle is acute (between 0 and 90 degrees), so the angle whose tangent is 1 is, of course, 45°. The difference between the two angles is 116.57-45=71.57°. We could have used the obtuse angle (180-71.57=108.43) but I think they would expect you to use the smaller angle as the obvious choice.
A picture helps to visualise what’s going on.