If the function is f(x)=|x| the graph is like a V where the vertex of the V is at the origin. The slope for x>0 is 1 and for x<0 the slope is -1. If we stretch the graph horizontal by a factor of 5, it means that instead of f(1)=1 we want to make the new f(5)=1 so x➝x/5. This makes the slope shallower because of the stretch.
We need to displace the vertex, which was at the origin, 3 units right. That means we want f(x) to be zero when x=3. So now we have x/5➝(x-3)/5 because the vertex is now (3,0) instead of (0,0). When x=8, f(8)=1 so the graph is displaced 3 units to the right. Finally, the vertical displacement downwards is achieved by subtracting 4 outside the absolute function: f(x)=|(x-3)/5|-4. The constant -4 is outside because the whole graph is shifted downwards for all x. The vertex is now at (3,-4) and f(8)=-3.
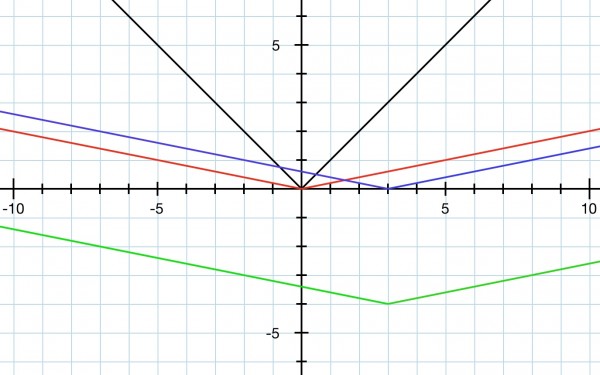
The picture shows in steps how the transformation takes place. The black line is the original function. The red line is the stretch. The blue is the shift to the right. The green line is the shift down, the final transformation.