Question

From city A to city B, a plane flies 650 miles at a bearing of N 48° E. From city B to city C, the plane flies 810 miles at a bearing of S 65° E. Find the distance from A to C and the bearing from A to C.

Answer 1

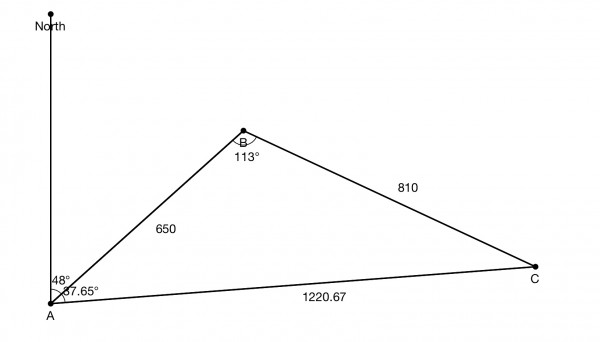
Angle B=48+65=113°.

AC=√(AB²+BC²-2AB.BCcos113)=√(650²+810²-2*650*810cos113)=

1220.67 miles approx. (Cosine rule)

Let θ be the bearing of C, then:

sin(θ-48)/810=sin113/1220.67, (sine rule)

sin(θ-48)=810sin113/1220.67=0.6108 approx.

So θ=48+37.65=85.65° (approx). The bearing is N85.65°E.