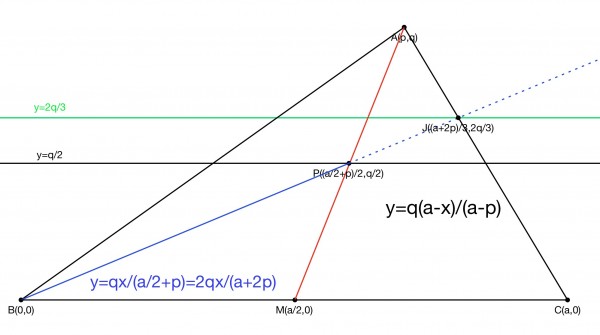
The picture above gives us a graphical solution to this proof.
The triangle has three vertices: A(p,q), B(0,0) and C(a,0). The base of the triangle AC therefore has a length of a. M(a/2,0) is the midpoint of AC, so AM is a median and P is its midpoint. The line y=q/2 bisects sides AB and AC as well as the median.
The x coord of P is the average of the x coords of M and A=(a/2+p)/2 so P has coords ((a/2+p)/2,q/2).
BP extended cuts AC at J, and we can find the coords of J be looking at the intersection of BJ and AC.
We can work out the equations of the lines BJ and AC.
First BJ: the slope is q/(a/2+p)=2q/(a+2p) so y=2qx/(a+2p).
AC: negative slope -q/(a-p) and y=q(a-x)/(a-p).
The lines intersect when 2qx/(a+2p)=q(a-x)/(a-p).
There is a common factor q which can be cancelled out. 2x(a-p)=(a-x)(a+2p).
2ax-2xp=a^2+2ap-ax-2xp, 3ax=a^2+2ap, 3x=a+2p, x=(a+2p)/3.
So y=2q/(a+2p) * (a+2p)/3=2q/3.
The green line y=2q/3 shows that
The height of the triangle and therefore the side AC is trisected QED.