TASK 1
Part 1
Let y=f(x)=(x+a)/b; x=g(y)=by-a=cy-d, so c=b and d=a.
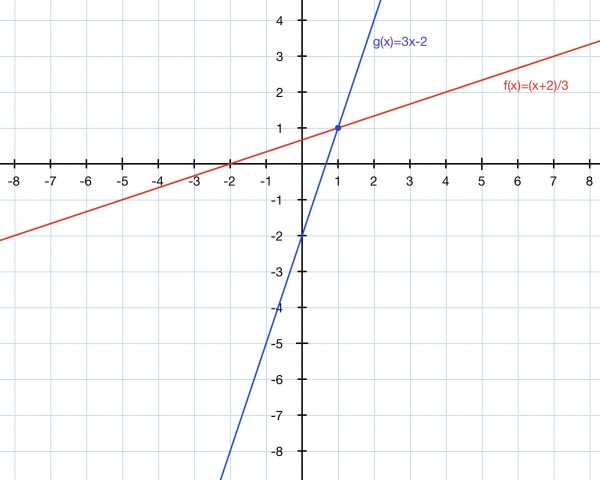
Let d=a=2 and c=b=3: f(x)=(x+2)/3 and g(x)=3y-2.
Part 2
y=f(x)=(x+2)/3; 3y=x+2; x=3y-2=g(y) so g(x)=3x-2, the inverse.
Part 3
g(f(x))=3f(x)-2=3(x+2)/3-2=x+2-2=x, so g(f(x))=x showing that f(x) and g(x) are mutual inverses.
| x= |
-2 |
-1 |
0 |
1 |
2 |
| f(x) |
0 |
1/3 |
2/3 |
1 |
4/3 |
| g(x) |
-8 |
-5 |
-2 |
1 |
4 |
Part 4
TASK 2
Part 1
(a) Let a=1, b=2, c=3, d=6: √x+2+3=6; √x-6=-5; (b) Let a=-1, b=2, c=3, d=4
(a) Multiply both sides by √x+6: x-36=-5(√x+6)=-5√x-30; x-36+30=-5√x; x-6=-5√x.
Square both sides: x^2-12x+36=25x; x^2-37x+36=0=(x-36)(x-1).
Part 2
(a) So x=36 or 1 (apparently). Substitute x=36 in the original equation: 6+2+3=6, 11=6 is not true. So x=36 is an extraneous solution; substitute x=1: 1+2+3=6 is true, so x=1 is the actual solution.
(b) -√x+2+3=4; -√x=-1; multiply both sides by -1: √x=1; square both sides: x=1. Substitute x=1 in the original equation: -1+2+3=4 is true. So x=1 is the solution.
Part 3
For (a) the act of squaring both sides resulted in creating an extraneous solution ((-5)^2=25=5^2). For (b) the solution was simpler and there was no ambiguity.
TASK 3
Part 1
John read 2 chapters of a book on Sunday. Each day of the week he reads one chapter more than the day before. How many chapters did he read on Saturday? How many chapters had he read altogether by the end of Saturday?
On Sunday he read 2 chapters; by Monday he'd read 3 more chapters; by Tuesday, 4 more chapters; by the following Saturday he'd read 8 more chapters.
a=2, d=1. The sequence is a, a+d, a+2d, ... For n days the term is a+d(n-1). (The sum is na+nd(n-1)/2.) Plug in a and d, and n=7: 2+6=8 for the 7th term. So he reads 8 chapters on Saturday. (The sum is 2*7+7*6/2=14+21=35 chapters.)
Part 2
On day 1 a bacterial culture contained 10000 bacteria. Each day the bacteria multiplied to increase their numbers by 10%. How many bacteria will there be on day 5?
a=10000 and r=1.1. The series is 10000, 11000, 12100, 13310, 14641.
The nth term is ar^(n-1)=10000*1.1^4.
Part 3
Each day the bacteria are given 1g of nutrient per 10000 bacteria. How much nutrient will they need for n days?
Sn is the total quantity of nutrient they will need after n days=1+1.1+1.1^2+...+1.1^(n-1)=(1.1^n-1)/(1.1-1)=10(1.1^n-1) grams.