How many students have used all three modes of transportation

Question

In a class of 40, 17 have ridden an airplane, 28 have ridden a boat. 10 have ridden a train, 12 have ridden both an airplane and a boat. 3 have ridden a train only and 4 have ridden an airplane only. Some students in the class have not ridden any of the three modes of transportation and an equal number have taken all three.

Answer 1

 

 

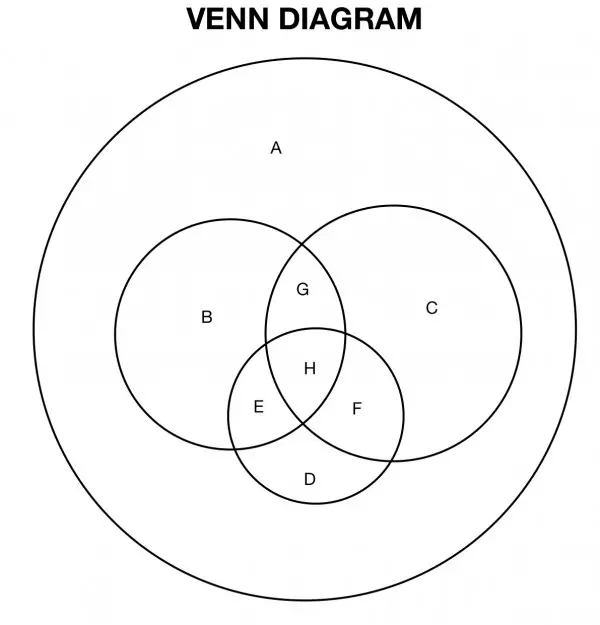
The above Venn diagram is split into 8 regions labelled A to H. The meaning of the regions:

A Students who have not used any of the named modes of transport

B Airplane only

C Boat only

D Train only

E Airplane and train but not boat

F Boat and train but not airplane

G Airplane and boat but not train

H All 3 modes of transport

Now we can put in some figures:

A+B+C+D+E+F+G+H=40 encompassing all the students in the class

A=H

D=3 train only

B=4 airplane only

B+E+G+H=17 airplane

C+F+G+H=28 boat

D+E+F+H=10 train

G+H=12 airplane and boat and possibly train

We can do some calculations:

C+F=16 because G+H=12, also B+E=5, but B=4, so E=1.

F+H=6 because D=3 and E=1.

4+C+3+1+F+H+G+H=40 because A=H, C+8+6+12=40, so C=40-26=14, therefore F=2 and H=6-2=4.

A=H=4 and the number of students using all three modes of transport is 4. Also G=12-H=8.