The total surface area of a cube is 6a^2, where a is the length of its side. A cube produces the maximum volume. If the area of the paper is completely used to form a cube 6a^2=11*8.5 and a=3.9476". The maximum volume is a^3=61.52 cu in approx.
If, however, the area of the paper could be used to cover a sphere of radius r, then 4πr^2=11*8.5, and r=√11*8.5/4π=2.7277" producing a sphere with volume=4πr^3/3=85.01 cu in approx.
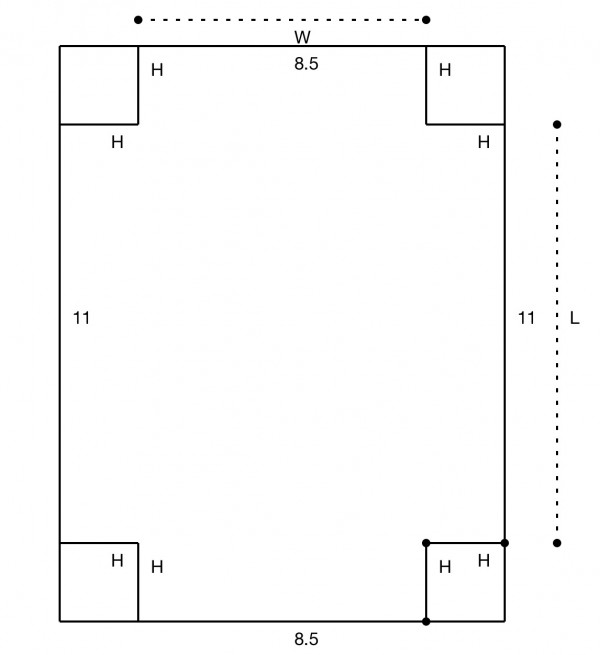
A more practical solution consists of folding the paper to form an open box. If we use L, W and H to represent the length, width and height of the box we can write: volume V=LWH; W+2H=8.5, L+2H=11, so we can express L and W in terms of H: W=8.5-2H, L=11-2H. V=H(11-2H)(8.5-2H)=93.5H-39H^2+4H^3.
dV/dH=93.5-78H+12H^2=0 at a maximum or minimum. The next derivative gives us -78+24H.
First, solve the quadratic: H=(78±√(78^2-4*12*93.5))/24=(39±√399)/24=4.9146" or 1.5854". By substituting these values into the second derivative, we can see that H=1.5854" is a maximum, while H=4.9146" is a minimum, and results in negative W and V. From H we can find L=11-2H=7.8292" and W=5.3292", V=66.1482 cu in. The paper has 4 squares side 1.5854" cut out from the corners. The paper then folds up to make an open box with the volume V.
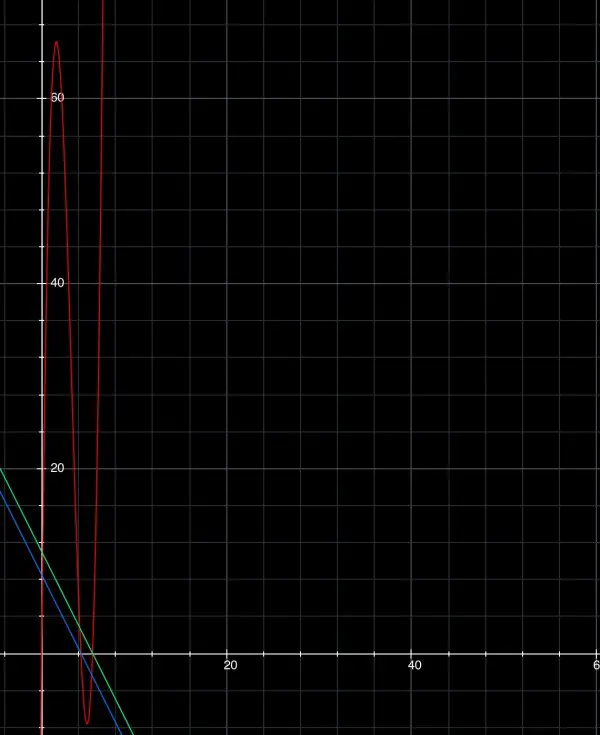
On the graph the red curve is the volume function V(H). The maximum is clear to see at 66.1482 cu in. The sloping lines show the width and length (W(H) in blue and L(H) in green), both of which must be positive to form a box with H. So the volume only has meaning when V, H, W and L are all positive (all in quadrant 1). When V is at a maximum, H, W and L are all positive. H is positive by being to the right of the origin and V, W and L are positive because they're all above the H-axis.