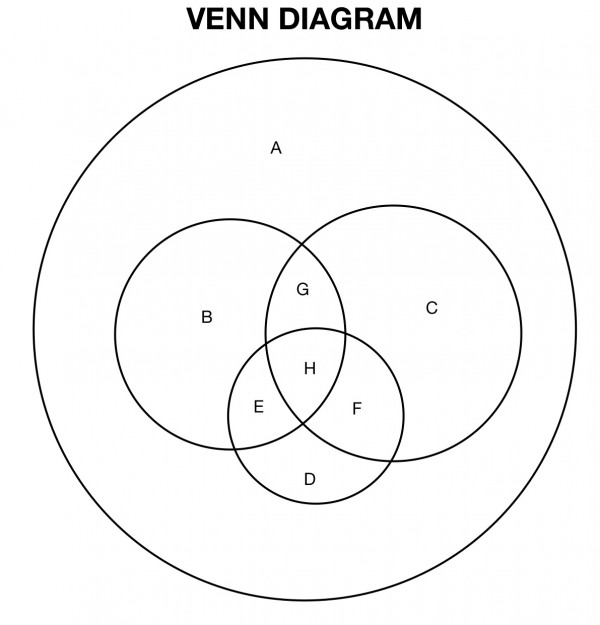
The Venn diagram above is split into 8 regions labelled A-H.
Each letter represents the number of people in the group. For example, B, C and D represent the number of people owning only a rabbit, cat or dog respectively.
In this problem the interlocking parts of the central circles represent owners of more than one pet.
B+G+H+E=16 rabbit owners
E+H+F+D=24 dog owners
G+H+F+C=17 cat owners
H=2 cat, dog and rabbit owners
F=cat and dog owners, G=cat and rabbit owners, F=G+1
E=9 dog and rabbit owners
A=0 do not own a dog, cat or rabbit
There is an ambiguity about the 39 pet owners: does this mean they own no more than one of cat, dog or rabbit; or it means they own at least one type of pet? In the first case B+C+D=39; in the second case B+C+D+E+F+G+H=39.
Now we can begin to plug in figures.
B+G=16-2-9=5, F+D=24-2-9=13, and G+1+D=13, so G+D=12
G+H+F+C=17; G+2+G+1+C=17; 2G+C=14
If we assume B+C+D+E+F+G+H=39, then (B+G)+(G+1+D)+(C+9+2)=39
5+13+C+11=39; C=39-(5+13+11)=39-29=10; 2G+C=14, so 2G=14-10=4 and G=2; and so there are 2 cat and rabbit owners. (Also, since B+G=5, B=3 who only own a rabbit; and D=12-2=10 only own a dog.)