Question

Find a normal vector of the curve 6x^2+2y^2+z^2 = 225 at the given point P : (5; 5; 5).

Answer 1

Find a normal vector of the curve 6x^2+2y^2+z^2 = 225 at the given point P : (5; 5; 5).​

The normal vector at a point 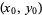on a surface 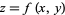is given by

(1)

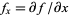where and 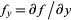are partial derivatives. and (x0, y0) = (5,5)

we have z = (225 - 6x^2 - 2y^2)^(1/2) = f(x,y), giving us

fx = -6x(225 - 6x^2 - 2y^2)^(-1/2),     and   fx(5,5) = -30(225 - 150 - 25)^(-1/2) = -30(25)^(-1/2) = -6

fy = -2y(225 - 6x^2 - 2y^2)^(-1/2),     and   fx(5,5) = -10(225 - 150 - 25)^(-1/2) = -10(25)^(-1/2) = -2

Therefore, N = | -6 |

                        | -2 |

                        | -1 |