obtain formula for r (inradius)

Question

?obtain formulas for r the radius of incircle and Ra,Rb and Rc, the radii of excircle of triangle ABC whose sides hes the lenght a,b and c

Answer 1

 

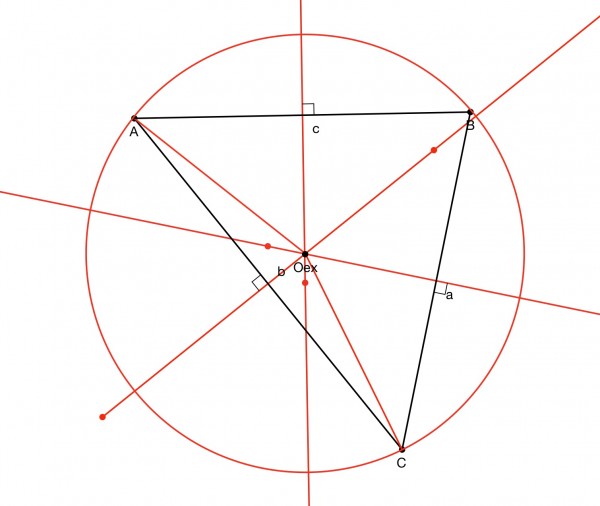
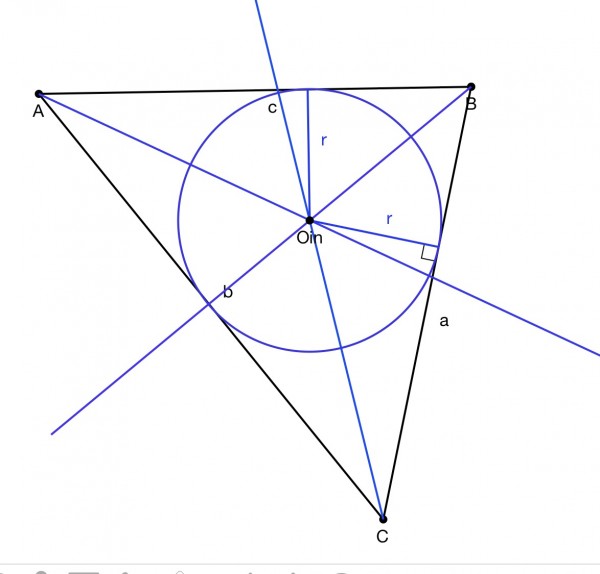
The pictures show the excircle and incircle of the same triangle ABC.

The centre of the excircle is the intersection of the perpendicular bisectors of the sides of the triangle, and the radius is the distance between the intersection point and any vertex of the triangle.

The centre of the incircle is the intersection of the angle bisectors of the triangle, and the radius is the length of the perpendicular from the intersection point to any side of the triangle, each of which is a tangent to the incircle.

EXCIRCLE

By the cosine rule, a^2=b^2+c^2-2bccosA, so cosA=(b^2+c^2-a^2)/(2bc).

The angle CAB=OAC+OAB and cosCAB=cos(OAC+OAB)=

cosOACcosOAB-sinOACsinOAB=

b/2r * c/2r - √((r^2-b^2/4)(r^2-c^2/4))/r^2, because OA=r, the radius of the excircle and the base of each right triangle is half the length of the side of the triangle.

Therefore, b/2r * c/2r - √((r^2-b^2/4)(r^2-c^2/4))/r^2=(b^2+c^2-a^2)/(2bc).

bc/4r^2-√((4r^2-b^2)(4r^2-c^2))/4r^2 = (b^2+c^2-a^2)/(2bc) and

(bc-√((4r^2-b^2)(4r^2-c^2)))/4r^2=(b^2+c^2-a^2)/(2bc).

So the radius of the excircle can be calculated from this formula.

INCIRCLE

Take vertex angle B bisected to form two congruent right triangles. We can write three equations:

rcot(B/2)+rcot(C/2)=a, rcot(B/2)+rcot(A/2)=c, rcot(A/2)+rcot(C/2)=b. 

Adding these equations together we get:

2r(cot(A/2)+cot(B/2)+cot(C/2))=a+b+c.

So r=(a+b+c)/(2(cot(A/2)+cot(B/2)+cot(C/2))).

C=180-(A+B), so C/2=90-(A+B)/2, and cot(C/2)=tan((A+B)/2). 

r=(a+b+c)/(2(cot(A/2)+cot(B/2)+tan((A+B)/2)).