Question

find critical points for z=sin (x*y)........then clacify them

Answer 1

z=sin(xy); ∂z/∂x=ycos(xy); ∂z/∂y=xcos(xy); ∂²z/∂x²=-y²sin(xy); ∂²z/∂y²=-x²sin(xy); ∂²z/∂x∂y=∂²z/∂y∂x=-xysin(xy).

∂z/∂x=0=ycos(xy) when xy=(2n+1)π/2; and ∂z/∂y=0=xcos(xy) when xy=(2n+1)π/2 (where n is an integer).

z=sin(xy)=1 or -1 when xy=(2n+1)π/2.

The second derivative test D(x,y)=(-y²sin(xy))(-x²sin(xy))-(-xysin(xy))²=0. The nature of the critical points is inconclusive.

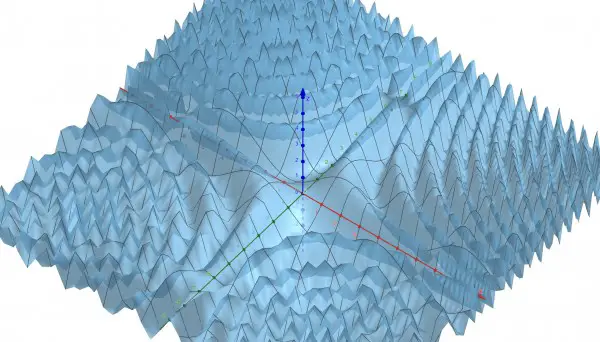
The actual surface of z is a set of continuous ridges (as in mountain ridges) forming a continuous rift (as valleys between the mountain ridges).

xy=(2n+1)π/2 is a set of rectangular hyperbolae, which forms a set of trajectories for mountain peaks and valleys.

So there are no local maxima and minima, just a set of ridges and valleys, infinitely long. The picture below shows the undulating surface. The hyperbolic shape formed by the mountains and valleys is evident in this representation.