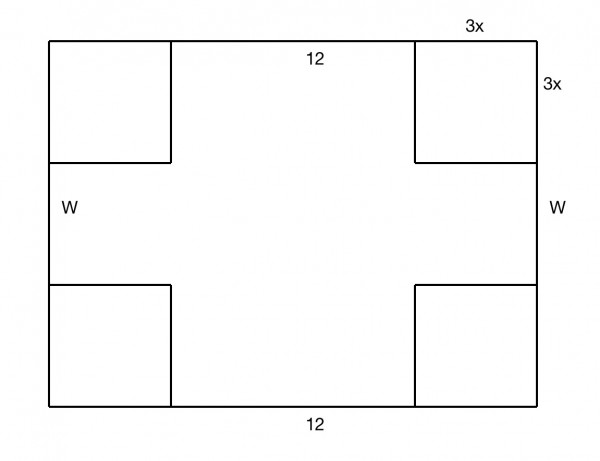
The cutouts reduce the length and width by 6x each: 12-6x and W-6x where W=width (not given).
The height of the box is 3x when the sides and ends are folded up.
The volume, V=3x(W-6x)(12-6x)=3x(12W-6xW-72x+36x^2)=36xW-18Wx^2-216x^2+108x^3=108x^3-18x^2(W+12)+36xW=18x(6x^2-(W+12)x+2W) cubic inches.
The domain of x must be so as to keep the sides with non-zero length. Therefore 12-6x>0, 12>6x or x<2.
And W-6x>0 so x<W/6. If W<12 then the domain is <W/6 otherwise it's <2.
If W=9, for example, the domain would be x<9/6 or x<3/2. V=18x(6x^2-21x+18)=54x(2x^2-7x+6) cu in.
If W=15, the domain would be x<2. V=18x(6x^2-27x+30)=54x(2x^2-9x+10) cu in.