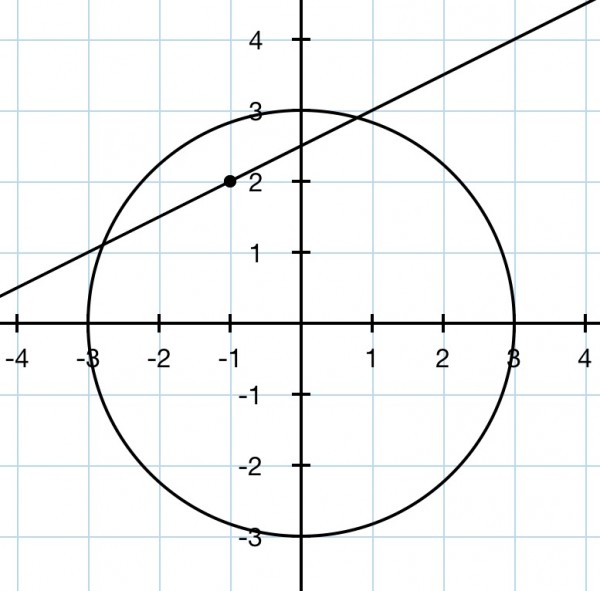
If y=ax+b is the equation of the chord, it intersects the circle when:
x^2+(ax+b)^2=9; x^2+a^2x^2+2abx+b^2=9; (a^2+1)x^2+2abx+b^2=9;
x^2+2abx/(a^2+1)+b^2/(a^2+1)=9/(a^2+1).
(x+ab/(a^2+1))^2=(9-b^2)/(a^2+1)+a^2b^2/(a^2+1)^2=((9-b^2)(a^2+1)+a^2b^2)/(a^2+1)^2=
(9a^2+9-b^2)/(a^2+1)^2.
The point (-1,2) lies on y=ax+b, so 2=-a+b, and b=a+2.
(x+a(a+2)/(a^2+1))^2=(9a^2+9-a^2-4a-4)/(a^2+1)^2=(8a^2-4a+5)/(a^2+1)^2.
x+a(a+2)/(a^2+1)=√(8a^2-4a+5)/(a^2+1)
The chord's midpoint is equidistant from the intersection points with the circle. The solution of the above quadratic involves the square root term on the right-hand side. Call this value X. So x=-a(a+2)/(a^2+1)±X.
Therefore, x=-a(a+2)/(a^2+1) is the midpoint where x=-1, thus -1=-a(a+2)/(a^2+1).
a^2+1=a^2+2a and a=1/2, so b=a+2=5/2. The equation of the chord must therefore be y=x/2+5/2 or 2y=x+5.
(X=√5/(5/4)=4√5/5 or 4/√5.)