Is this (A) (x^2+1)/x^2=27 or (B) x^2+(1/x^2)=27? The question as presented contains ambiguities in the text. The table below shows various solutions depending on how the text is interpreted.
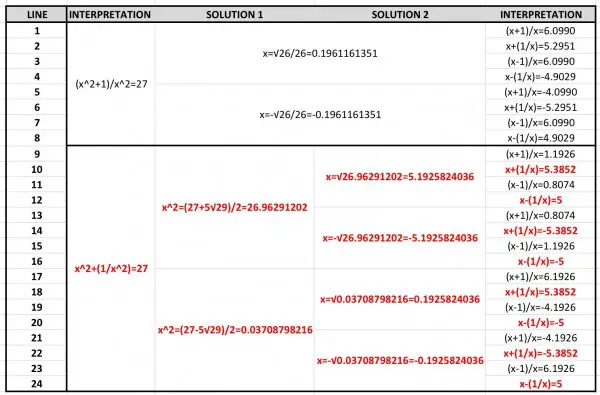
It would appear from the table that one particular interpretation was intended, because the last column for lines 12, 16, 20 and 24 contains an integer as a solution (5 or -5). If we track back to the second column we can see what the initial interpretation was: x^2+1/x^2=27. (The track is shown in bold red.) We can also see that x-(1/x) is what the question is probably looking for, and, by deduction, we can assume that the question is also looking for x+(1/x). We can presume that the question was intended to contain a hidden property that caused an integer to appear uniquely in one of the solutions.
We can track through to discover the hidden property.
Note: (x^2+1/x^2)^2=x^4+2+1/x^4=729, so x^4+1/x^4=727,
and similarly, (x^2-1/x^2)^2=x^4-2+1/x^4=727-2=725, substituting for x^4+1/x^4. So, x^2-1/x^2=±√725=±5√29=(x-1/x)(x+1/x).
Therefore, one of these factors is ±5 and the other is ±√29.
The table confirms the results and the combination of + and - signs.