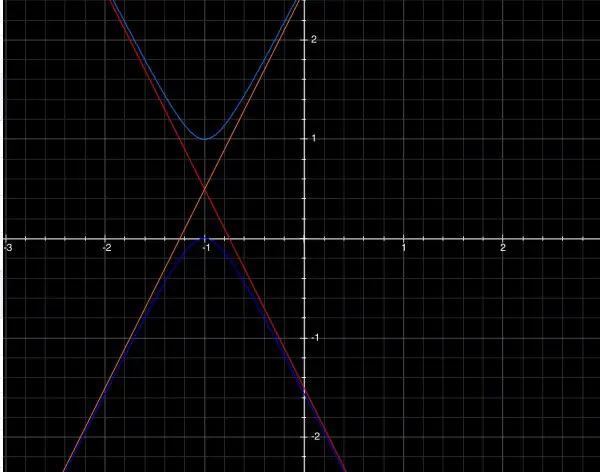
The general equation of a hyperbola is (x-h)^2/a^2-(y-k)^2/b^2=+1. The asymptotes are the solutions of (x-h)^2/a^2-(y-k)^2/b^2=0, ((x-h)/a+(y-k)/b)((x-h)/a-(y-k)/b)=0. For +1 the hyperbola is horizontal, so are its foci, and for -1 it's vertical, so are its foci. The line joining the foci is perpendicular to the conjugate axis, which is parallel to the x axis in this case (perpendicular to the y axis), so the foci are located vertically in line, parallel to the y axis. The equation is therefore (x-h)^2/a^2-(y-k)^2/b^2=-1. (h,k) is the centre or origin of the hyperbola, and represents the displacement of the axes from (0,0).
Whether the hyperbola is horizontal or vertical doesn't alter the asymptotes. So (x-h)/a+(y-k)/b)=4x-2y+5 is one of the asymptotes; or (x-h)/a-(y-k)/b)=4x-2y+5. This asymptote has a positive slope, so, since the asymptotes form an X, it's the / one. The other asymptote has negative slope \. Therefore, x/a=4x and y/b=2y, so a=1/4 and b=1/2. The constant 5=-4h+2k.
To find the vertices, put x=h, then y-k=+b=+1/2. The vertices are (h,k+1/2) and (h,k-1/2), having a common x coord, h. So h=-1, and k is given by 5=4+2k, k=1/2. Therefore, the equation of the hyperbola is 16(x+1)^2-4(y-1/2)^2=-1. This expands to 16x^2+32x-4y^2+4y+16=0. The \ asymptote has the equation 4(x+1)+2(y-1/2)=4x+2y+3=0. A graph of the hyperbola is shown below.