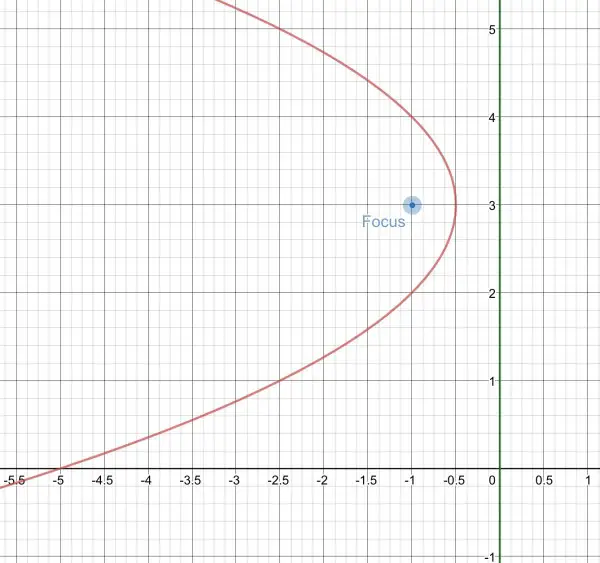
The picture should help to clarify the details below.
The directrix lies outside the parabola and x=0 is a vertical line (the y axis shown in green) so the parabola is lying on its side. The axis of symmetry is perpendicular to the directrix.
The focus (shown as a blue point) lies on the horizontal axis of symmetry inside the parabola, so the y coord of the focus is the axis of symmetry, that is, y=3.
The horizontal distance between the vertex and the focus is the same as the horizontal distance between the vertex and the directrix line. So we know the vertex is halfway between the focus and the directrix along the axis of symmetry y=3. The directrix meets the axis of symmetry at (0,3) and the focus is at (-1,3). The average of the x coords is (0-1)/2=-½, the halfway position. The vertex is at (-½,3).
The parabola has its arms pointing to the left because the focus at (-1,3) is to the left of the vertex at (-½,3). This tells us the equation of the parabola is of the form x-h=-a(y-k) where (h,k) is the vertex (-½,3) and a=1/4f where f is the distance of the focus and the vertex=½, so a=½.
The equation of the parabola is x-(-½)=-½(y-3)², which is x+½=-½(y-3)².
We can expand this:
x+½=-½(y²-6y+9),
2x+1=-(y²-6y+9)=-y²+6y-9,
2x+y²-6y+10=0.