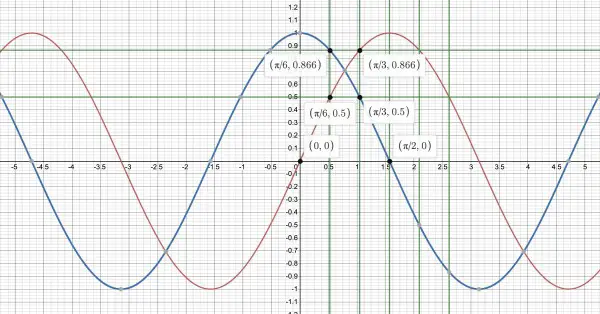
The blue curve is y=cosθ and the red curve is y=sinθ. You can see that the two curves are displaced by a fixed distance apart and some points are shown by the green cross-wires:
cos(0)=sin(π/2)=1; cos(π/6)=sin(π/3)=√3/2; cos(π/3)=sin(π/6)=½. 0=π/2-π/2; π/6=π/2-π/3; π/3=π/2-π/6, and in general cos(π/2-θ)=sin(θ) and conversely sin(π/2-θ)=cos(θ).
(a) In the graph below the solid vertical green line represents an arbitrary value of θ. Where it intersects the blue curve is cos(θ) (shown as the point (1,0.5403)). The vertical broken green line represents 3π/2+θ, and where it intersects the red curve is sin(3π/2+θ) (shown as the point (5.712,-0.5403)). We can see from this that sin(3π/2+θ)=-cos(θ), since the horizontal broken green lines are equidistant from the θ-axis, making the y coordinates the negative of each other. We can also see that cos(θ)=cos(-θ) so that sin(3π/2+θ)=-cos(-θ), because cos(θ) is an even function (is symmetrical about the y-axis).
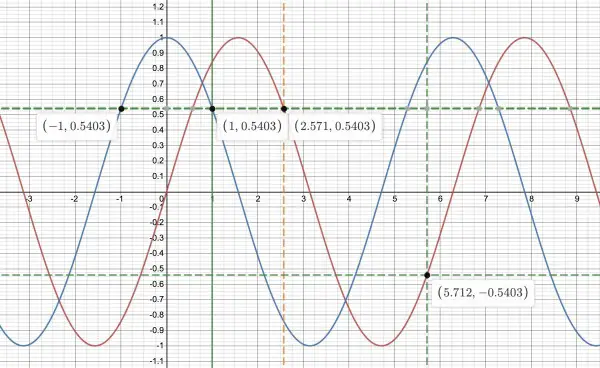
(b) The broken orange line represents π/2+θ, and it intersects the red curve at sin(π/2+θ) which has the same value as cos(θ) as shown by the upper horizontal broken green line.
If you imagine the assembly of the three vertical lines to be shifted bodily left or right (changing θ, π/2+θ and 3π/2+θ and the intersections), the relationships sin(3π/2+θ)=-cos(-θ) and sin(π/2+θ)=cos(θ) are always true.