If i rolled 6 different dice what the probabilty on each sum? 6-36 how would i solve?

Question

rolling six different dice what is the probability for each sum from 1-36?

Answer 1

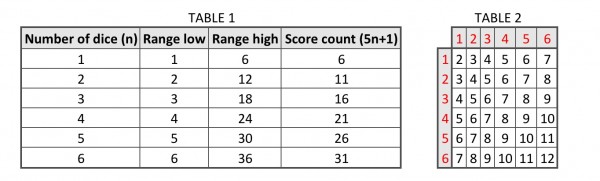
In this problem we're looking for a pattern from which to derive a formula to find the required probabilities. See TABLE 1.

n (the number of dice) determines how many different scores we can get, shown under the score count=5n+1. To find the number of ways of arriving at a particular score, and hence the probability, we need to do further analysis. TABLE 2 shows all possible scores for 2 dice.
S(2,2)=S(2,12)=1; S(2,3)=S(2,11); 2; S(2,4)=S(2,10)=3; ...The individual die scores are shown in red, while the cells are the sums of these scores. There are 6²=36 cells in the table and we can list all 11 possible scores as a function S(n,x) where n=number of dice=2 and x is the score. We'll see how the domain x is defined below.

In this case S(n,x)=S(n,7n-x)=x-(n-1)=x+1-n, that is, n=2, and 2≤x≤7.

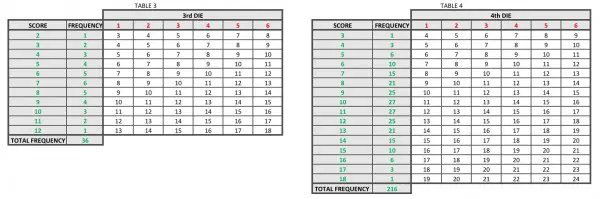
In the first two columns of TABLE 3 we have the scores with their frequencies derived from TABLE 2.

From these frequencies we can calculate probability, P(n,x)=S(n,x)/6ⁿ=(x+1-n)/6ⁿ. Note that ∑P(n,x)=1 (sum of frequencies=36, shown at the bottom of the first two columns of TABLE 3). So this formula is true for n=2, but not necessarily true for other values of n, although it may be possible to derive a general formula from this formula. ∑P(n,x)=1 always applies to other values of n, but S(n,x) needs to be revised for general usage.

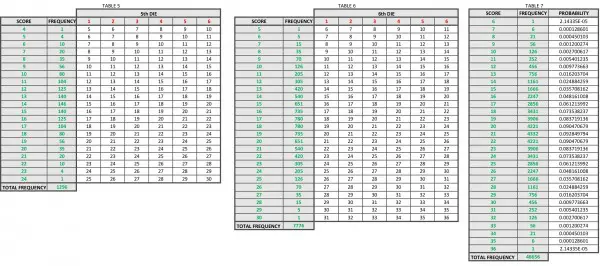
TABLES 4, 5, 6 show the result of adding the 4th, 5th and 6th dice using the same method of calculating frequencies. So TABLE 4 uses frequencies derived from TABLE 3, TABLE 5 uses those from TABLE 4, and TABLE 6 uses those from TABLE 5. The way to do this for TABLE 4, for example, is to inspect TABLE 3 for a specific score in the body of the table and then add together the numbers in the FREQUENCY column. Let's take the score of 7. It appears 5 times in TABLE 3. In the frequency column we have the numbers 1-5, which sum to 15, so in TABLE 4 against 7 in the SCORE column the FREQUENCY column contains 15. This rule applies to all scores in TABLES 4-7.

TABLE 7 provides the frequencies (S) and the probabilities for all possible scores resulting from rolling 6 dice. The probability (P) as a fraction can be found by dividing the frequency by 46656 (6⁶). For example, the probability of the score 21 is 4332/46656=361/3888=0.092849794. A copy of this table follows in the comment. This is the reference table providing the answer to the question.

Comments

This table has been reproduced in case you can’t read it in the answer.