f(x)={ x+3 if x<-2
-2x-3 if x≥-2 } is a piecewise function.
When x=-2, x+3=-2+3=1 and -2x-3=4-3=1. This means that there is continuity at x=-2 which is where the two pieces of f(x) join without a break. Another way of writing f(x) would be f(x)=x+3 up to but including x=-2 and f(x)=-2x-3 otherwise.
Let's work out the intercepts separately for the two pieces.
f(x)=x+3=0⇒x=-3 for the x-intercept (horizontal); and f(0)=3 for the y-intercept (vertical).
f(x)=-2x-3=0⇒x=-3/2 for the x-intercept (horizontal); and f(0)=-3 for the y-intercept (vertical).
Now we need to consider which intercepts apply. Only intercept values of x less than -2 apply for f(x)=x+3, so x=-3 is a valid x-intercept for this piece. Only intercept values of x≥-2 apply for f(x)=-2x-3, so x=-3/2 is a valid x-intercept for this piece.
f(0) can only apply to f(x)=-2x-3 because x=0 is greater than x=-2, so the y intercept is y=f(x)=-3.
This should be clearer by looking at the graph:
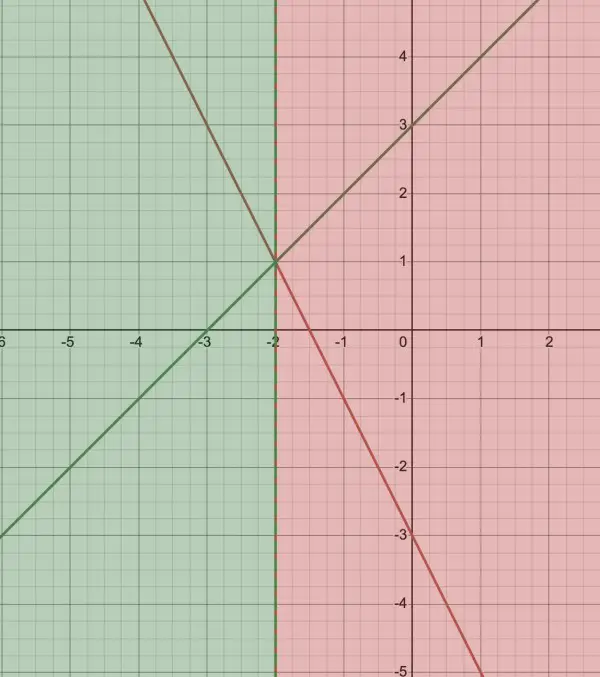
The green line is f(x)=x+3 but the only piece of interest is the part of the line that lies in the green shaded region. The red line is f(x)=-2x-3 but the only piece of interest is the part of the line in the red shaded region. The x-intercepts can be seen where the green line crosses the x-axis and where the red line crosses the x-axis, each in its own region.
The y-intercept is in the red region only, that is, where f(x)=-2x-3. The green line intercepts the y-axis but it's not in the green region so it doesn't apply.
We can also see the extent of the y values. y cannot exceed 1 because the red line would be in the green region and the green line would be in the red region, and the regions don't match the colours of the lines. So (-2,1) is the maximum of f(x). The range is therefore (-∞,1). Every value of y<1 has two corresponding values of x. For example, y=-1 corresponds to x=-1 and x=-4, one point for each line. When y=1 (f(x)=1) there is only one point on the red line (-2,1), since the green line doesn't allow x=-2 (x has to be less than -2).