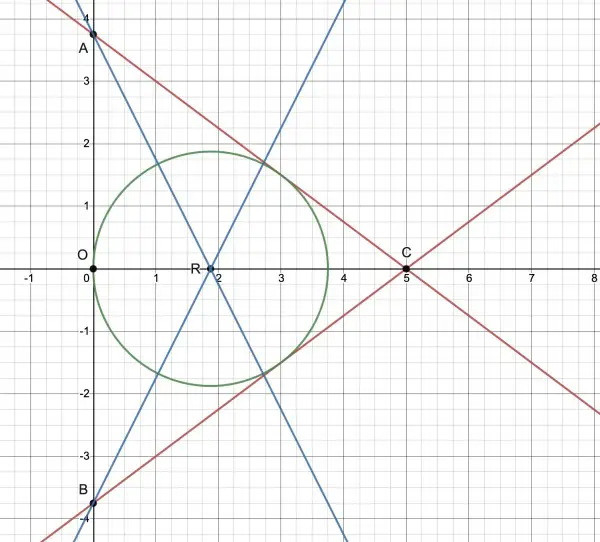
The in-centre is the centre of the in-circle of the isosceles triangle formed by the y-axis (x=0) and the two given lines. The y-intercepts are given by plugging x=0 into the two line equations, so one intercept is A(0,15/4) and the other is B(0,-15/4). The x-intercepts are the same at C(0,5). If O is the origin (0,0) then OC=5 and OA=OB=15/4. The angles BAC and ABC are congruent because ABC is isosceles. Let these angles be x.
OC is perpendicular to AB so tan(x)=5/(15/4)=4/3. The in-centre is the intersection of the angle bisectors of the vertex angles. AC, BC and AB are tangents of the in-circle. If we let t=tan(x/2) then tan(x)=2t/(1-t2)=4/3, so 4-4t2=6t, 4t2+6t-4=0=2(2t-1)(t+2), therefore tan(x/2)=½ or -2. If the angle bisectors meet at R, then OR is the radius of the in-circle. tan(x/2)=½=OR/OA=OR/OB. OA=OB=15/4, so OR=15/8, which is the radius of the in-circle. Since OR lies on OC, its coordinates are (15/8,0).